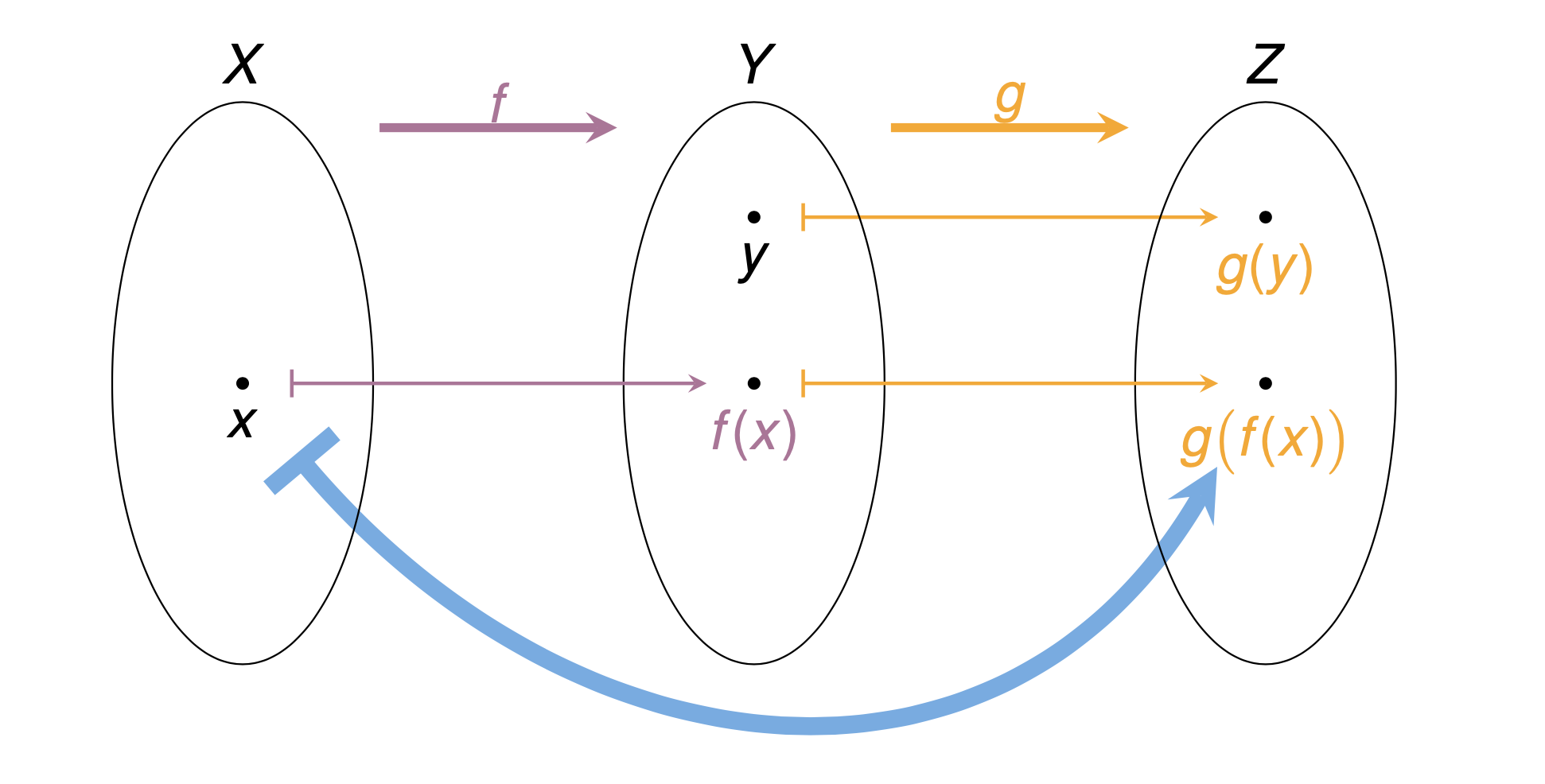
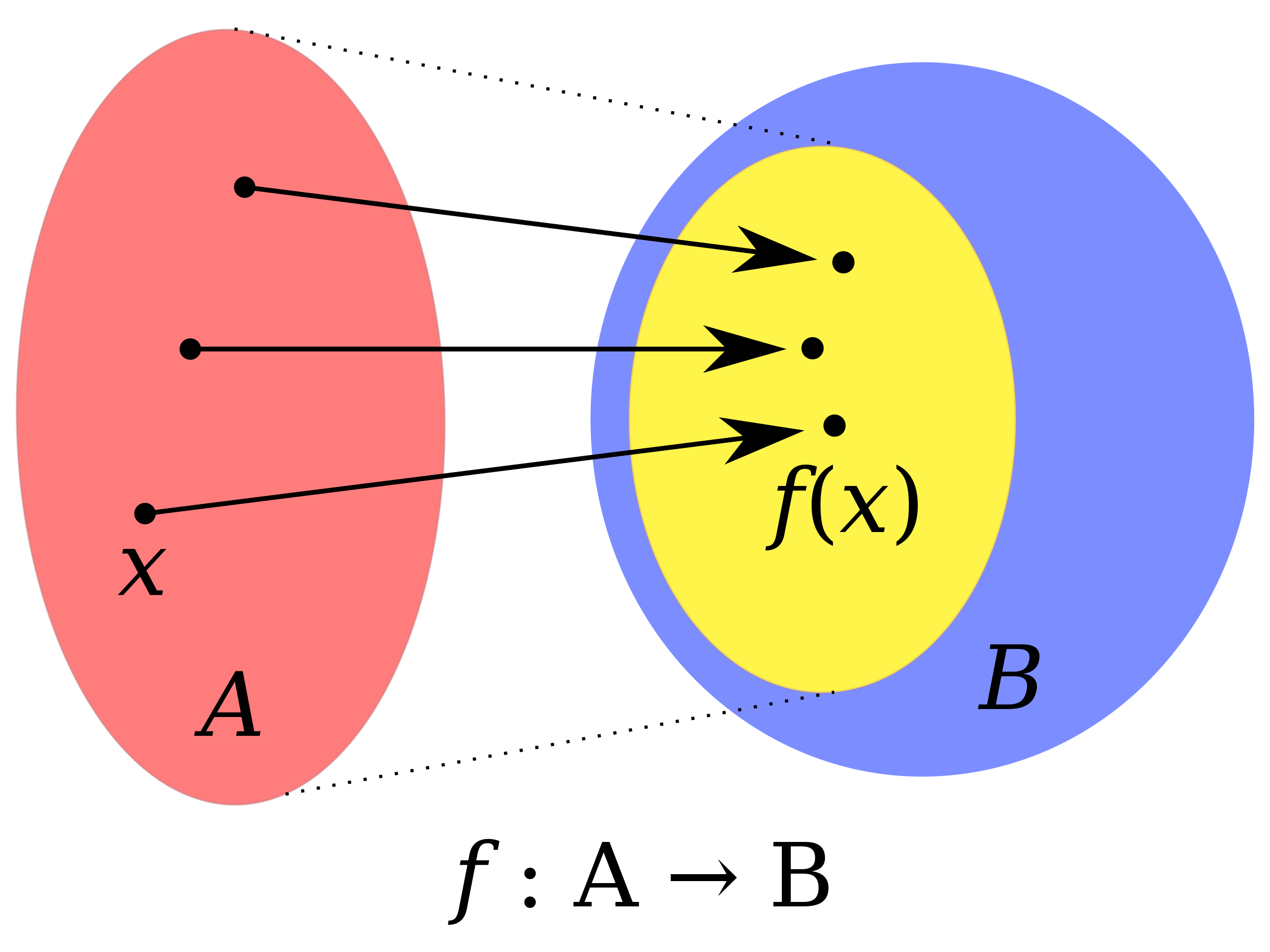
Lectures
You can download the lectures here. We will try to upload lectures prior to their corresponding classes.
-
An introduction to 301
tl;dr: We discuss the structure of the course, additional resources, grading policy, responsibilities, support in the first half. In the second half, we discuss what proofs are and why we need them.
[slides]
Suggested Readings: Chapter 0 of the textbook
-
 Propositions with Lean
Propositions with Lean
tl;dr: We use the proof assistant Lean as propositional logic.
[Lean code]
Open the attached lean code file with your favourite text editor. I recommend Sublime text or VSCode.
Extras
-
Some popular science articles about computer formalization of mathematics you might enjoy: ‘
How clos are computers to automating mathematical reasoning – Quanta Magazine
Mathematicians welcome computer-assisted proof in ‘grand unification’ theory – Nature
Proof Assistant Makes Jump to Big-League Math – Quanta Magazine
-
If you are interested in learning more about Lean, your are welcome to join the Lean Prover community online on Zulip chat.
-
Write your proofs of week 2 extra exercises in Lean.
-
-
 First Order Logic -- Variables, Predicates, and Quantifiers
First Order Logic -- Variables, Predicates, and Quantifiers
tl;dr: We explore some of the limitations of the propositional logic. We see how the first order logic gives us the right tools to overcome these limitations.
[slides]
Suggested Readings: Sections 1.2 and 1.3 of the textbook
-
 First Order Logic -- Natural Deduction
First Order Logic -- Natural Deduction
tl;dr: We introduce natural deduction for first order logic.
[slides]
Suggested Readings: Sections 1.2 and 1.3 of the textbook
-
 Proof Strategies
Proof Strategies
tl;dr: We use natural deduction to get a bird's eye view of the structure of our mathematical proofs.
[slides]
-
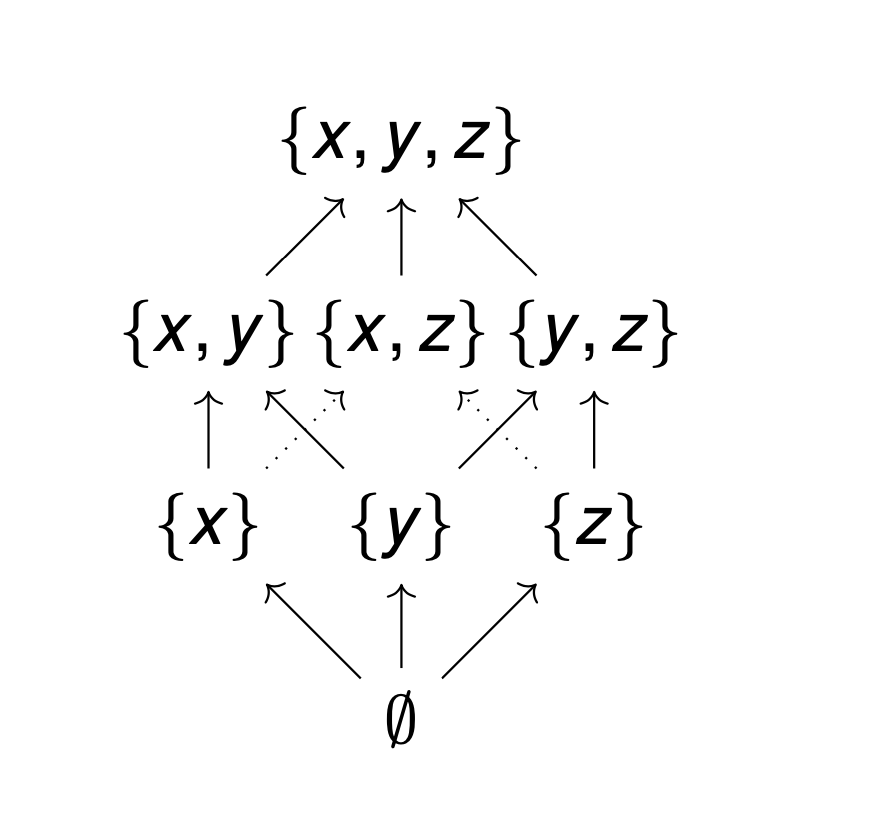 Relations
Relations
tl;dr: We introduce the notions of ordered sets, partially ordered sets, and equivalence relations with tons of examples.
[slides]
Suggested Readings: Chapters 3 and 5 of the textbook
-
 Isomorphisms
Isomorphisms
tl;dr: When are two sets the same? Take 2
[slides] [handout]
Suggested Readings: Chapters 3 and 5 of the textbook
Extras
- Barry Mazur, When is one thing equal to some other thing?
-
 Induction on natural numbers
Induction on natural numbers
tl;dr: We learn about natural numbers and the principles of induction and least element.
[notes]
Suggested Readings: Chapter 4 of the textbook
-
 Recursion
Recursion
tl;dr: We learn about recursion. We use recursion to define addition(+) and we prove 1+1=2.
[slides] [handout]
Suggested Readings: Chapter 4 of the textbook
Cool stuff to do with recursion: Recursion ‘Super Power’ (in Python) - Computerphile