Lesson (I)

Table of contents

1. Isomorphisms
2. Bijections

Isomorphisms

An isomorphism between two sets $A$ and $B$ is a pair of functions \[ f \maps A \to B \,\,\, \text{and} \,\,\,\, g \maps B \to A \] such that $g\circ f = \id_A$, and $f\circ g = \id_B$.

In such a situation, we call $f$ an inverse of $g$ and $g$ and inverse of $f$.

We can think of functions $f$ and $g$ above as no data-loss ``processes’’, e.g. conversion of files to different format without data being lost.

The sets $A$ and $B$ are said to be isomorphic in case there exists an isomorphism between them. In this case, we use the notation $A \iso B$. We say sets $A$ and $B$ are uniquely isomorphic if there is a unique pair of mutually inverse functions $f$ and $g$ which witness this isomorphism.

For exmaple, any two singletons are uniquely isomorphic. If we have sets $\set{🥕}$ and $\set{⛄}$ then they are isomorphic since we can find functions $f\maps \set{🥕} \to \set{⛄}$ defined by $f(🥕) = ⛄$ and $g(⛄) = 🥕$. This pair of function is an isomorphism since $f(g(⛄)) = f(🥕) = ⛄$ and $g(f(🥕)) = g(⛄) = 🥕$. Moreover, $f$ and $g$ are uniquely determined.

Isomorphisms are revetible processes and they let us to go back and forth between two different sets without loss of information. In fact, there is a sense in which somorphisms, rather than equality of sets is the correct notion of sameness of sets: For instance in the example of $\set{⛄}$ and $\set{🥕}$ both sets Since all the singletons are isomorphic

Challenge

We also have a function $\set{🥕} \to \set{🥕,⛄}$ which assigns 🥕 to 🥕. Does this function have an inverse? Why not?

Theorem (Inverses are Unique)

An inverse of a function, if it exists, is unique.

Let us give a less trivial exmaple of isomorphism of sets: Previously, we defined the cartesian product $A \times B$ of two sets $A$ and $B$ to consists of all the pairs $(a,b)$ where $a \in A$ and $b \in B$. Now, we show that the order of forming products does not matter, the sets $A\times B$ and $B \times A$ are isomorphic. To show this, we need to construct a pair of inverse functions \[ f\maps A \times B \to B \times A \quad \text{ and } \quad g\maps B\times A \to A\times B \, .\] We define $f$ by the assignemnt $(a,b) \maps (b,a)$ and $g$ by the assignemnt $(b,a) \maps (a,b)$. Now, \[ f \circ g (b,a) = f(a,b) = (b,a) \quad \text{ and } \quad g \circ f (a,b) = g(b,a) = (a,b) \, , \] for all $a \in A$ and $b \in B$. Therefore, by function extensionality, we have $ g\circ f = \id_{A \times B}$, and $f\circ g = \id_{B\times A}$. We conclude that \[ A \times B \iso B \times A \, .\]

Challenge

1. Show that for all sets $A$, we have $A \times 1 \iso A$.
2. Show that for all sets $A,B,C$ we have $A \times (B \times C) \iso (A\times B) \times C$.
3. Show that for all sets $A,B,C$ we have $(A \times B) \times C \iso C \times (B\times A)$.

Challenge (Commutativity and Associativity of Disjoint Unions)

1. Show that for all sets $A,B$ we have \[ A + B \iso B + A \, \]
2. Show that for all sets $A,B,C$ we have \[ A + (B + C) \iso (A + B) + C \, .\]

Challenge

Is it true for all sets that $1 + A \iso A$? If not, find a condition about $A$ which forces $1 + A \iso A$ to be true.

Weaker Notions

The inverse functions we introduced above are sometimes called two-sided inverses; the reason behind it is clear, it does not matter in which order we compose the functions $f$ and $g$, whether $f$ appears to the right of $g$ or to the left of it, the result is identity. There are however weaker notions of inverse which are quite useful. Here are the two most important ones:

• A retract (aka left inverse) of a function $f \maps A \to B$ is a morphism $r \maps B \to A$ such that $r \circ f = \id_A$. In this case we also say $A$ is a retract of $B$.
• A section (aka right inverse) of function $f \maps A \to B$ is a morphism $s \maps B \to A$ such that $f \circ s = \id_B$.

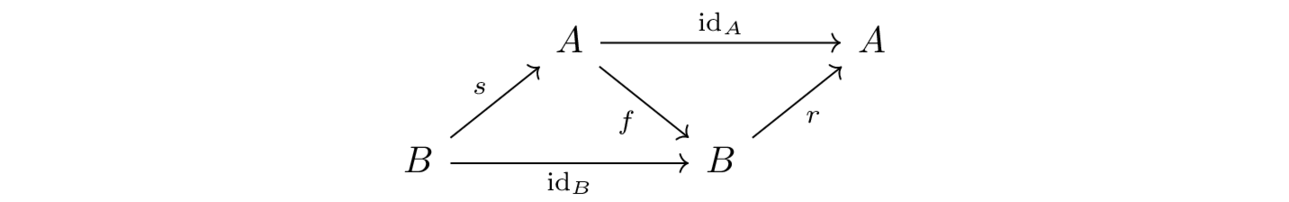
Challenge (Canonical Function From Sum to Union)

There is a canonical function $A + B \to A \cup B$ which takes $(a,0)$ to $a$ and $(b,1)$ to $b$.

1. Is this function an isomorphism?
2. Does this function have a section?

Bijections

A function $f \maps A \to B$ is injective (also called one-to-one) whenever the following sentence holds. \[ \forall a,b \in A,\, f(a) = f(b) \Rightarrow a=b \] An injective function is said to be an injection.

Theorem (Sections are injective.)

Every function with a retract is injective.

Proof

Suppose $f \maps A \to B$ is function with a retract $r \maps B \to A$. Therefore, $r \circ f = \id_A$. Suppose $f(a) = f(\pr{a})$. It follows that \[ a = \id_A (a) = r \circ f (a) = r (f(a)) = r(f(\pr{a})) = r \circ f (\pr{a}) = \id_A (\pr{a}) = \pr{a} \, .\]

Challenge

Is the converse of the above theorem also true?

Theorem

Let $f \maps A \to B$ be a function. If $f$ is injective and $X$ is inhabited, then $f$ has a retract.

The dual concept to injection is surjection. A function $f \maps X \to Y$ is surjective (aka onto) whenever \[ \forall y \in Y,\ \exists x \in X,\ f(x) = y \] holds. A surjective function is said to be a surjection.

Challenge (Surjectivity and Inhabitedness)

Show that the function $\cons{X} \maps X \to 1$ is surjective if and only if $X$ is inhabited.

Theorem (Retractions are surjective.)

Every function with a section is surjective.

Challenge

Prove that the canonical function $A + B \to A \cup B$ is a surjection.

A function which is both injective and surjective is said to be bijective. An injective function is said to be an bijection.

Theorem

Every isomorphism of sets is a bijection.

Proof

Suppose $f \maps A \to B$ is an isomorphism. Then $f$ has an inverse $g \maps B \to A$. The function $g$ serves both as a section and as a retraction for $f$. Therefore, by theorems above $f$ is both injective and surjective, and hence it is bijective.

Challenge

Does the converse of the last theorem hold as well? If yes, give a proof, and if no, supply a counter-example.

Challenge

Show that if $A$ and $B$ are disjoint sets (i.e. their intersection $A \cap B$ is empty) then the canonical function $A + B \to A \cup B$ is in fact an isomorphism.