Lesson (I)

Table of contents

1. Functions, Act I
2. Functions, Act II
3. Equality of Functions
4. Sequences
5. Partial Functions

Functions, Act I

Functions will be the highest hill we climb in this course. In one respect, everything we have learned so far will seem to be a prelude for functions. They will give us the best views of all other concepts. Think of this: what would propositions be without the rules of inference? Same thing for functions: what would sets be without functions?

Functions will give a precise way to relate one set to the other.

As every other concept in this course, functions can be reduced to sets, that is a function can be defined as a particular set. But this will not be the intuitive way we think about them. We will first introduce an informal and yet workable semi-definition of function. As we shall soon see, this informal definition surprisingly allows to develop a whole lot of theory about functions and prove interesting results about them.

In the second act, we shall try to formalize this intuition into a proper definition.

We think of function $f$ from a set $A$ to a set $B$ as a specification of a unique element $f(a)$ in $B$ for each $a$ in $A$. The uniqueness is expressed logically by saying that if $a=a’$ in $A$ then $f(a) = f(a’)$ in $B$.

We write $f \maps A \to B$ to denote the assertion that $f$ is a function with domain $A$ and codomain $B$. We also say that the function “assigns” the element $f(a)$ to the element $a$.

Therefore, to describe a function, one must specify

• its domain,
• its codomain, and
• the effect of function upon an arbitrary element of its domain. and prove that the specification is
• total, i.e. it is defined on all elements of domain, and
• deterministic, i.e. it gives the same output when given the same input.

For instance the “squaring’’ function on the set of real numbers is specified in either of the following ways:

• $f \maps \RR \to \RR$ where $f(x) = x^2$ for every real number $x$, or
• $x \mapsto x^2 \maps \RR \to \RR$, or
• $\lambda x. x^2 \maps \RR \to \RR$.

Note that we distinguish between functions $\sin \maps [0, 2\pi ] \to \RR$ and $\sin \maps \RR \to \RR$ since their domains are different sets; the first function cannot be applied to $3\pi$. Also the functions $\sin \maps \RR \to \RR$ and $\sin \maps \RR \to [-1,1]$ are distinct this time because of different codomains. We assign the same elements to each real number, are different since their codomains are different. And, since they are different, we better give them different names; we reserve the name $\sin$ for the function with domain $\RR$ and codomain $[-1,1]$.

How to define a function?

The simplest way to define a function is to give its value at every $x$ with an explicit well-defined expression.

Here are few examples:

• Let $f \maps \mathbb{N} \to \mathbb{N}$ be the function defined by $f(n) = n + 1$, that is $f = \lambda n . n+1$.
• Let $g \maps \mathbb{R} \times \mathbb{R} \to \mathbb{R}$ be the function defined by $g(x,y) = x^2 + y^2$.
• The assignment to each real number the greatest integer less than or equal to it. We call this function the floor function. We denote this function by $\lfloor{-}\rfloor \maps \RR \to \ZZ$.
• The assignment to each real number the least integer greater than or equal to it. We call this function the ceiling function. We denote this function by $\lceil{-}\rceil \maps \RR \to \ZZ$.

Challenge

Decide whether the following are functions, and give reasons for your answers:

• The assignment $e \maps \NN \to \NN$ given by $n \mapsto $ “the $(n+1)$-th prime number”.
• The assignment $f \maps \Prop \times \Prop \to \Prop$ which assigns to a pair of propositions $P$ and $Q$ a proposition $R$ such that $P \land R \implies Q $.
• The assignment $g \maps \RR \to \RR$ which assigns to a real number $x$ a real number $y$ such that $y^2 = x$.
• The assignment $g’ \maps \CC \to \CC$ which assigns to a complex number $z$ a complex number $w$ such that $w^2 = z$.
• The assignment $h \maps \QQ \to \QQ$ given by $h(y) = 1/y$.
• The assignment $j\maps \NN \to \NN$ given by $m \mapsto d$ where $d$ is a divisor of $m$.
• The assignment $k$ which assigns to a natural number $n$ set of a natural numbers $S$ the proposition “there is a member of $S$ which divides $n$”.

It is sometimes convenient to define a function using different specifications depending on the form of the elements of the domain. For example, the absolute value function $|{-}| : \mathbb{R} \to \mathbb{R}$, defined for $x \in \mathbb{R}$ by \[ |x| = \begin{cases} x & \text{if } x \ge 0 \\ -x & \text{if } x \le 0 \end{cases} \] As it is clear from this example, we have two branches for the specification of the absolute value function, each branch has a domain (a subdomain of the original domain) and an specification for the elements of this subdomain.

When specifying a function $f \maps X \to Y$ by cases, it is important that the following conditions are met:

• The specifications are exhaustive: given $x \in X$, at least one of the conditions on $X$ must hold; and
• The specifications are compatible: if any $x \in X$ satisfies more than one condition, the specified value must be the same no matter which condition is picked.

We see that the compatibility condition is met for the absolute value function at the point $x=0$.

The Identity Functions

There is a wonderful yet very simple function which is defined in the same way for every set. This is the so-called identity function of that set. For a set $A$, we define a function $\mathrm{id}_A \maps A \to A$ which assigns to an element $a$ itself! Therefore, $\mathrm{id}_A (a) = a$.

The Inclusion Functions

Suppose $A \subseteq B$. There is a rather trivial function $\iota \maps A \to B$ which takes an el

Composition of Functions

The main idea of composition of functions is to create compound functions from simpler functions which can do more tasks. A function can be implemented in different ways, but once it is implemented, we can forget about the details of its implementation and concentrate on how it interacts with other chunks. The operation of composition gives us an incredibly powerful tool to focus on these interaction of functions.

You might already be familiar with operation of composition of functions from piping in Unix based OS, say in a Linux or Mac terminal. The pipe takes output from one command and uses it as input for another. The general form of piping is as follows: cmd1 | cmd2 where cmd1 and cmd2 are commands to be performed on some file. Here is an example of piping: Say that you want to sort the list of names in your contacts file contacts.txt. First, let’s look at the contents as they are in the file before sorting. We can do this with the command cat, and indeed cat contact.txt outputs the list of contacts:

Ulrich
Christian Moosbruger
Rachel 
Ermelinda Tuzzi
Walter
Bonadea
Paul Arnheim
Diotima 
Agathe
Franz Joseph
Clarisse

We think of command cat as a function whose input is a .txt file and its output is a string of characters on the screen (but saved nowhere). Now, suppose we want to sort our contacts by their first names in an alphabetical order. We do this by typing cat contacts.txt | sort into the terminal. Here cat first reads the content of contacts.txt and then the command sort sorts it:

Agathe
Bonadea
Christian Moosbruger
Clarisse
Diotima 
Ermelinda Tuzzi
Franz Joseph
Paul Arnheim
Rachel 
Ulrich
Walter

If we have a long contact list and we suspect there could be duplicate entries, we can use the command uniq to remove possible duplicates:

cat contacts.txt | sort | uniq

Finally, we save the sorted contacts into a new file contacts_sorted.txt:

cat contacts.txt | sort | uniq > contact_sorted.txt

Now, let us abstract away from this particular example and introduce the operation of composition for general functions. Suppose $f \maps A \to B$ and $g \maps B \to C$ be are functions. We define a new function $g \circ f \maps A \to B$ by letting \[ g \circ f (x) \defeq g(f(x)) \, .\] The function $g \circ f$ is called the composition of $f$ and $g$ which we also call “$f$ composed with $g$” (or “$g$ after $f$”). Often when there is no risk of confusion mathematicians dispense with $\circ$ in the notation above and simply write $g f$ for the composition of $f$ and $g$. The image below illustrating the composition of two functions is form “Proof and the Art of Mathematics” by J.D. Hamkins.

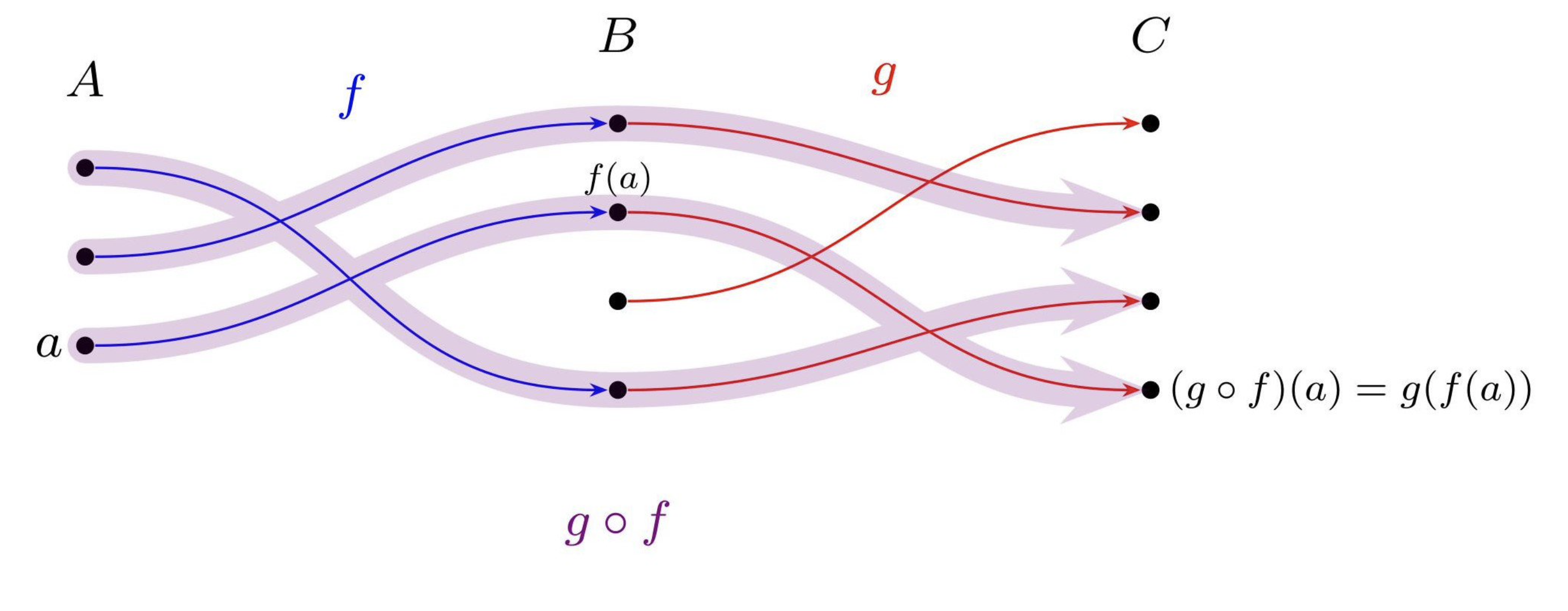
In our piping example at the beginning of this section, all we did was composing three functions $c,s,u$ where $c$ is for cat, $s$ is for sort, and $u$ for uniq, and applying $u \circ (s \circ c)$ to the input contact_sorted.txt. ¹

We capture the high-level information of composition by a diagram: Note that here we abstract away form the variable $x$. Also, note that the order of composition is somewhat confusing; the syntactic order does not match the diagrammatic order. In the diagram above, $f$ appears to the left of $g$ while in the syntactic expression of composition $g \circ f$, the function $f$ appears appears on the right. Nevertheless, they both mean the same thing: in order to evaluate the expression $g(f(x))$ you first evaluate $f$ on input $x$, and then evaluate $g$. The function $g$ waits for the the result $f(x)$ of application of $f$ to the input $x$ and once that is available, $g$ applies to the value $f(x)$.

Challenge

We introduced the absolute value function $|{-}| \maps \mathbb{R} \to \mathbb{R}$ on real numbers. Suppose we have a set $X$ and a function $f \maps X \to \RR$. What is the result of composition of $f$ and $|{-}|$?

The composition of functions introduced above has two important properties:

• Unitality: For any function $f \maps A \to B$, we have $f \circ \id_A = f$ and $\id_B \circ f = f$.
• Associativity: For any functions $f \maps A \to B $, $g \maps B \to C$ and $h \maps C \to D$, we have \[ h \circ (g \circ f) = (h \circ g) \circ f \, , \] as functions from $A$ to $D$.

Challenge

Prove unitality and associativity of composition of functions.

Challenge

Think what associativity means for the example of piping.

Functions of Many Arguments (Multivariable Functions)

So far our functions take a single argument as their input, but the functions of many arguments are abound. A function of many arguments can depend on two or more arguments. Most physical laws can be expressed as functions of many arguments: for instance the pressure (P) of an ideal gas is a function of its temperature (T) and volume (V). And, kinetic energy of a particle is a function of its mass and velocity.

Suppose $f$ is a function (a total deterministic rule) which assigns to elements $a$ of $A$ and $b$ of $B$ and element $f(a,b)$ of $C$. Since we have the operation of cartesian product on sets we can in fact consider $f$ as a function from the cartesian product $A \times B$ to $C$. Therefore we write $f \maps A \times B \to C$.

Composition of Functions of Many Arguments

Suppose we have function $f \maps A_1 \times A_2 \times A_3 \to B_1$ and $g \maps B_1 \times B_2 \to C$ and $t \maps C \to D$ and $h\maps C \times D \to E$. Take for inputs $a_1 \in A_1$, $a_2 \in A_2$ and $a_3 \in A_3$ and $b \in B_2$ and $c \in C$. We can feed these inputs to the functions above and get elements $f(a_1, a_2, a_3) \in B_1$ and in turn feed this and $b$ to the function $g$ to get $g(f(a_1, a_2, a_3), b) \in C$, and then feed the latter and $t(c)$ to $h$ to get $h(g(f(a_1, a_2, a_3), b), t(c))$ in $E$. Therefore the composed operation takes \[ a_1, a_2, a_3, b, c \] as inputs and outputs \[ h(g(f(a_1, a_2, a_3), b), t(c)) \, .\] Schematically we can picture this operation as stacking boxes (operations) on top of each other in such a way that the wires (carrying input/output) connect:

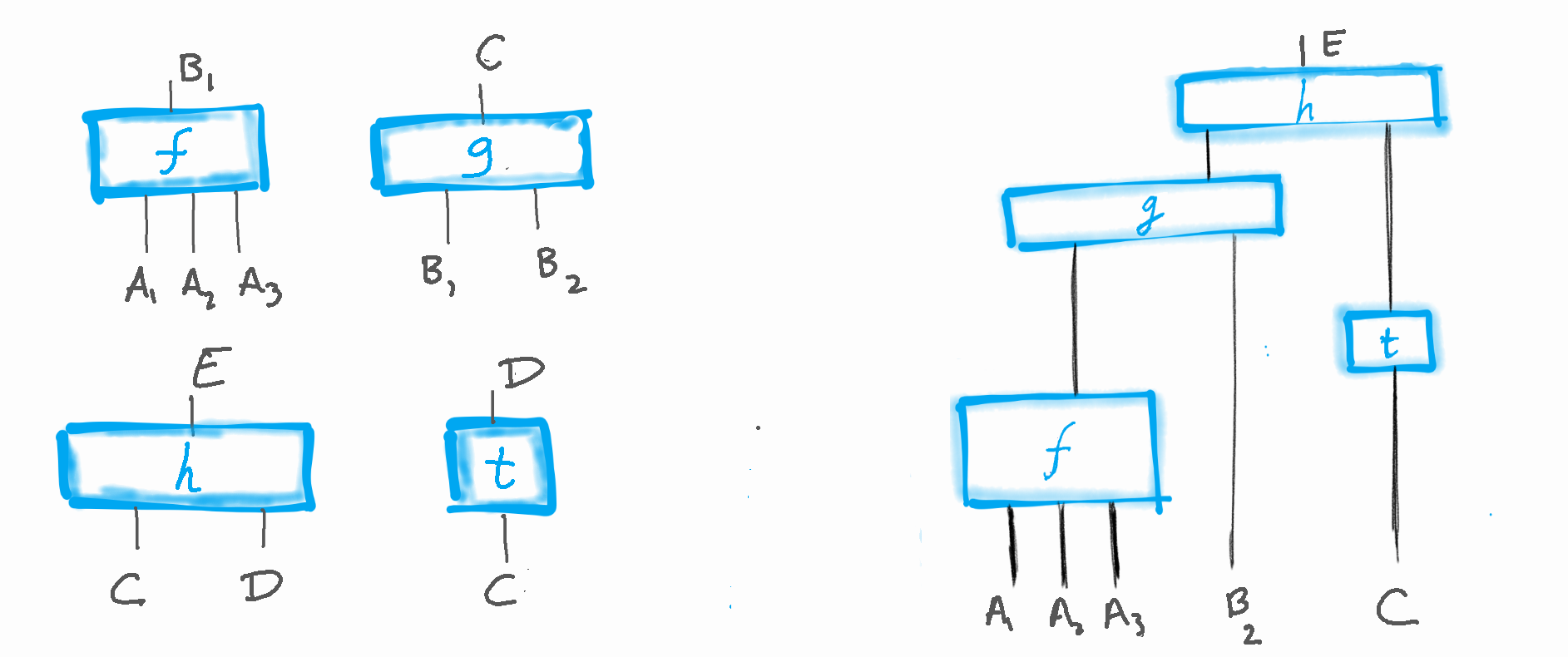
Is there a way to use the composition of functions to construct the operation which corresponds to the picture above, abstracting away from the input variables $a_1, a_2, a_3, b, c$? We should be able to compose functions $f,g,t,h$ to get a function from $A_1 \times A_2 \times A_3$ to $E$, but how? Surely we cannot write $g \after f$ since the codomain of $f$ does not match the domain of $g$. What’s the solution? The first step is to find a function, using composition, to produce $g(f(a_1, a_2, a_3), b)$ for every input $a_1, a_2, a_3, b$. The domain of such function would be $A_1 \times A_2 \times A_3 \times B$ and the codomain would be $B_1 \times B_2$. To actually construct it though, we need to extend the operation of cartesian product (introduced for sets) to functions.

Challenge

Extend the operation of cartesian product (introduced for sets) to functions in such a way that $\id_A \times \id_B = \id_{A \times B}$.

To see how we define the product of functions, expand the button below:

Functions of Many Arguments From Functions of Single Argument

A function of many arguments can be obtained by iteration of application of a function of a single argument. This insight is often attributed to the Russian mathematician Moses Ilyich Schönfinkel, but it was already in use by Frege. Today it is known as “currying”, a tribute to Haskell Curry who later introduced it in his work independently. If we have a function, say $f$ which depends on two variables $a$ and $b$, we can form the expression $f(a,b)$. Now fix $a$ and define $F_a$ to be a function of $b$ given by $F_a (b) = f(a,b)$. In lambda notation,
\[ F_a = \lambda b\, . \, f(a,b)\] Now, define \[ F = \lambda a\, . F_a\] which is a function of $a$. Both $F_a$ and $F$ are functions of a single argument. But, now we have
\[ (F a) \, (b) = F_a (b) = f(a,b) \, .\]

In the section on function sets we make this idea itself into a function!

Constant Functions

We say a function $f \maps A \to B$ is constant if for all $a,a’ \in A$ we have $f(a) = f(a’)$. What this definition says is that no matter what the inputs are the outputs are always equal. Suppose the set $A$ has $m$ elements and the set $B$ has $n$ elements. How many constant functions $A \to B$ do you think there are?

Challenge (Constant Functions)

1. For every set $A$ prove that there is a unique function from $A$ to $1$ where $1 = \set{\star}$. Show that this function is constant.
2. Show that the identity function $\id \maps \emptyset \to \emptyset$ is constant.
3. Suppose $f \maps A \to B$ and $g \maps B \to C$ are functions. Show that if either $f$ or $g$ is constant then their composition $g \circ f$ is constant. Is the converse true?

Nomenclature Thenceforth, the constant function $X \maps 1$ shall be denoted by $\cons{X}$.

Challenge

Prove that for a function $f \maps A \to B$, if the set $A$ is inhabited then $f$ is constant if and only if the following sentence holds: \[ \exists b \in B \, \forall a \in A \, f(a) = b \]

Challenge

Prove that a function $f \maps A \to B$ is constant if and only if there is a factorization of $f$ as in below for some $b \in B$. Do you need the Law of Excluded Middle in your proof? Can you do without it?

Function Restrictions

Suppose $f \maps A \to B$ is a function and $U \subseteq A$. We can restrict the function $f$ to $U$, that is we only restrict $f$ to those elements of $A$ which are already present in $U$. For instance if we restrict the absolute value function to the set of positive real numbers we obtain the identity function on positive real numbers. We would like to have a notation for the restriction operation on functions: If we have a function $f \maps A \to B$ we denote by $f \restriction U$ the restriction of $f$ to $U$. Note that $f \restriction U \maps U \to B$.

Challenge

Suppose $f \maps A \to B$ is a function and $V \subseteq U$ and $U\subseteq A$. Prove that \[ (f\restriction U) \restriction V = f \restriction V \, , \] as functions from $V$ to $B$.

Function Extension

Dual to the notion of function restriction is the notion of function extension. Suppose $f \maps A \to B$ is a function and $A \subseteq E$. We say a function $g \maps E \to B$ extends $f$ if $g \circ \iota = f$ as shown in the diagram below.

Challenge

Unlike restriction, extension is not an operation. Why?

Functions, Act II

In this lesson, we follow our foundationalist tendency to define the notion of function in terms of the notion of relation (which was defined as a set).

In Functions, Act I, We defined functions by specification of a unique element of the codomain to every elemenet of domain. We can implement this specification by relating every element of the domain to a unique element of the codomain, that is we include in our relation all pairs $(a,b)$ where $b=f(a)$.

Consider for instance the function $f \maps \NN \to \NN$ given by the specification $f(n) = n^2$. We can encode this specification as a relation $R_f$ on the set $\NN$ of natural numbers where $R_f(n,n^2)$ holds. Therefore, the extension of this relation is a subset of the cartesian product $\NN \times \NN$, ii.e. $\ext{R_f} \subset \NN\times \NN$ and it includes all pairs $(n, n^2$) where $n \in \NN$.
\[ \ext{R_f} = \set{(0,0), (1,1), (2,4), (3,9), \ldots} \]

The set $\ext{R_f}$ is sometimes known as the graph of function $f$, and is also denoted by $\graph(f)$.

Therefore, functions can be seen as relations. But these relations are not any relations; they are special. This motivates the following definition.

A binary relation $R$ on $A$ and $B$ is functional if for every $a$ in $A$ there exists a unique $b$ in $B$ such that $R(a,b)$. We can express this formally by the following sentence \[ \big( \forall a \exists b \, R(a,b) \big) \wedge \big( \forall a \forall b \forall c \, (R(a,b) \wedge R(a,c) \To b=c) \big) \]

If $R$ is a functional relation, we can define a function $f_R \maps A \to B$ by setting $f_R(a)$ to the unique $b$ in $B$ such that $R(a,b)$ holds.

Challenge

Show the converse: prove that if $f \maps A \to B$ is a function, the relation $R_f(x, y)$ defined by $f(x) = y$ is a functional relation.

We have now characterized functions in terms of relations. This is a common move in mathematics. We think we understand a concept $\mathfrak{R}$ (e.g. the concept of relation) well enough. We want to use this understanding to understand a new concept $\mathfrak{F}$ (e.g. e.g. the concept of function). We find a way to see $\mathfrak{F}$ as $\mathfrak{R}$. But, that is not enough; we also want to determine which of the instance of $\mathfrak{R}$ are instances of $\mathfrak{F}$ under this new way of seeing $\mathfrak{F}$ as $\mathfrak{R}$. Usually we find a finite number of properties, say $P_1, \ldots P_n$ (called characteristics) which compeletely characterize which of $\mathfrak{R}$’s correpond to $\mathfrak{F}$’s. In other words, we prove a “characterization” theorem which states that any object $R$ which is an instance of concept $\mathfrak{R}$ and for which $P_1(R), \ldots, P_n(R)$ holds, is an instance of concept $\mathfrak{F}$.

Challenge

Suppose $A$ is a set. Prove that the relation corresponding to the identity function on $A$ is the identity relation on $A$. Can you describe the graph of the idenity function on $A$?

Challenge

Find a relation corresponding to the constant function $\cons{X} \maps X \to 1$.

Challenge

For which of the following specifications of sets $X,Y$ and $G\subset X\times Y$ is $G$ a graph of a function?

1. $X=\mathbb{N}, \, Y=\mathbb{N}, \, G=\set{(x,y)\in \mathbb{N}\times \mathbb{N} \mid x \text{ divides } y }$
2. $X=\set{n \in \NN \mid n \geq 1}, \, Y=\mathbb{N}, \, G=\set{(x,y) \in X \times \mathbb{N} \mid y \text{ is the greatest power of 2 dividing x} }$
3. $X=\mathbb{R}, \, Y=\mathbb{R}, \,G=\set{(a,a^2) \mid a \in \mathbb{R} }$
4. $X=\mathbb{R}, \, Y=\mathbb{R}, \, G=\set{(a^2,a) \mid a \in \mathbb{R} }$
5. $X=\set{r \in Q \mid r \geq 0}, \, Y=\set{r \in Q \mid \geq 0}, \, G=\set{(x^2,x) \mid x \in X }$
6. $X=\set{r \in Q \mid r \geq 0}, \, Y=\QQ, \, G=\set{(x^2,x) \mid x \in X }$

Composition of Functions Agrees with Composition of Relations

We saw in Composition of Relations that we can compose relations provided that the codomain of the first relation is the same as the domain of the second one. More precisely, if we have relation $R$ from set $A$ to $B$ and a relation $S$ from $B$ to $C$, then we form the relation $S \circ R$ to be a relation from $A$ to $C$.

Also, we saw how to compose functions in Composition of Functions. One might wonder that now we know how to see functions as relations, if these two compositions agree. Let us make this question more precise: Suppose $f \maps A \to B$ and $g \maps B \to C$ are functions. Consider the corresponding relations $R_f$ and $R_g$. What is the exact nature of the relation between $R_g \circ R_f$ and $R_{g \circ f}$?

Challenge

1. Prove that the relation corresponding to the composite function $g \circ f$ is equivalent to the composite relations $R_g \circ R_f$, that is, \[ \forall x\in X \, \forall z \in Z \, \big( x \, R_{g \circ f} \, z \iff x \, (R_{g} \circ R_{f})\, z \big) \]
2. Conclude from the result of the last part that $\ext{R_{g \circ f}} = \ext{R_{g} \circ R_{f}}$.

Challenge

For a function $f \maps A \to B$ and a subset $U \subseteq A$, describe the operation of restriction of $f$ to $U$ in terms of the corresponding relation $R_f$.

Equality of Functions

In the lesson on equality of sets, we discussed what it means for two sets to be equal. In the previous lesson, we observed how functions can be defined as functional (binary) relations, and since (binary) relations were defined as subsets (of cartesian products of their domain and codomain), the equality of two functions is induced from the equality of their corresponding functional relations. Therefore, if $f \maps X \to Y$ and $g \maps X \to Y$ are two functions then
\[ f=g \iff R_f = R_g \]

Theorem (Function Extensionality)

Two functions $f \maps X \to Y$ and $g \maps X \to Y$ are equal if and only if the sentence \[ \forall x \in X \, f(x) = g(x) \] is true.

This means, two functions are equal if and only if once fed the same input, their outputs are equal. The latter condition is sometimes called “point-wise” equality.

Proof

Let us denote by $R_f$ and $R_g$ the functional relations corresponding to $f$ and $g$, respectively. Suppose $f=g$. Therefore, $R_f = R_g$ as sets, by definition of function equality. Suppose $x$ is an arbitrary element of set $X$. We know that $(x,f(x)) \in R_f$ by definition of $f(x)$. But since $R_f = R_g$, we have $(x,f(x)) \in R_g$. We also have that $(x,g(x)) \in R_g$ by definition of $g(x)$. Since $R_g$ is a functional relation, there must however be a uniqe $y \in Y$ such that $(x,y) \in R_g$. It follows that $f(x) = g(x)$. Since $x$ was arbitrary, we conclude that that the sentence $\forall x \in X \, f(x) = g(x)$ holds. Conversely, suppose the sentence $\forall x \in X \, f(x) = g(x)$ holds. We want to show that $R_f = R_g$ as sets. Take an arbitrary element $(x,f(x))$ in $R_f$. By our assumption, $f(x) = g(x)$, and therefore, $(x,f(x)) = (x,g(x))$. But, $(x,g(x))\in R_g$. Hence, $(x,f(x)) \in R_g$. Since $(x,f(x))$ was arbitrary, we conclude that $R_f = R_g$. $\qed$

As a result of this theorem, we give two examples where in each example we have different expressions, but the function which they express are the same:

• The absolute value function: \[ \begin{cases} x & \text{if } x \ge 0 \\ -x & \text{if } x < 0 \end{cases} \quad \text{ and } \quad \begin{cases} x & \text{if } x \ge 0 \\ -x & \text{if } x \le 0 \end{cases} \]

Challenge

Use function extensionlity to show that for any set $A$ there is a unique function $\emptyset \to A$.

Commuting diagrams of functions

We say a square of sets and functions commutes

whenever $g \circ f \circ h = k$

Challenge

For functions $f,g \maps A \to B$ express the equality $f=g$ in terms of commutativity of a certain square.

Sequences

A sequence in a set $A$ is simply a function $a \maps \NN \to A$. The sequence $a$ assigns to every natural number $n\in\NN$ an element $a(n)\in X$. By convention people write $a_{n}$ for $a(n)$ and $(a_{n})$ for the sequence $a \maps \NN \to A$. The notation $(a_{n})$ communicates the idea of a sequence as an infinite list. Note that in lists, in contrast to sets, the order of appearance of elements matter.

Occassionally, we may speak of a sequence $(a_{n})$ in a subset $U\subseteq A$, by this we mean a sequence in $A$ whose every term is in $U$, that is, $\forall n\in\NN,a_{n}\in U$.

Here are some examples of sequences:

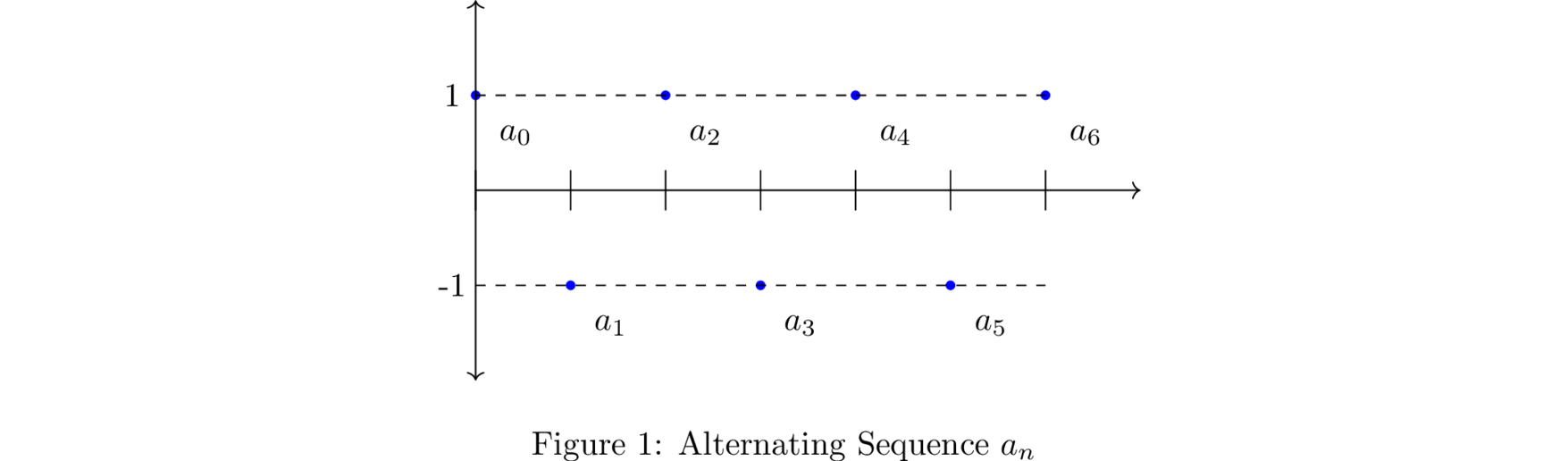
• $(a_{n})$ in $\ZZ$ where $a_{n} = (-1)^{n}$; the sequence terms are $1,-1,1,-1,\ldots$
• $(b_{n})$ in $\QQ$ where $b_{n} = n/(1+n)$; the sequence terms are $0,\frac{1}{2},\frac{2}{3},\frac34,\ldots$

A sequence $(a_{n})$ in $A$ is constant if the function $a \maps \NN \to A$ is constant.

A sequence $(a_{n})$ is eventually constant if \[\exists N\in\NN, \, \forall n\in \NN, \, n\ge N \To a_{n}=a_{N} \, .\]

Challenge

Prove that any constant sequence is eventually constant.

Subsequences

In the depiction of the sequence of $(a_{n}) = (-1)^{n}$, a subsequnce is any infinite selection of some (possibly all) of the blue dots selected in the same order as in the original sequence. For instance, a subsequence can be \[ \begin{cases} a_n & \text{if } n \le 6 \\ 1 & \text{if } n > 6 \end{cases} \]

However, this does not guarantee that the macro behaviour of the sequence remains the same when we pass over to a subsequence: While the sequence $a_n$ is alternating, its subsquence consisting of only $1$’s does not.

Alright, we get the intuition of subsequnce. But, we need a proper definition if we are going to prove statements about subsequnces rigorously.

Suppose $(a_{n})$ is a sequence in $A$. A subsequence of $(a_{n})$ is given by an endo-function $k \maps \NN \to \NN$ which is strictly increasing in the sense that if $m < n$ then $k(m) < k(n)$.

Alrighy! How does this definition match our intuition from the blue dots? We think of the function $k$ in the definition as generating a new sequence (by composition!) $a \circ k \maps \NN \to A$ which we write as $(a_{k_{n}})$. We regard the sequence $a \circ k \maps \NN \to A$ as a subsequence of $a \maps \NN \to A$ since the terms of $a \circ k$ are \[ a_{k(0)}, a_{k(1)}, a_{k(2)}, \ldots \] which are surely included in the list of terms below. \[ a_0, a_1, a_2, \ldots \, \]

Here are more examples of subsequences:

• The subsequence $(a_{p_n})$ of $(a_n)$, where $a_n$ is the sequence of even numbers (i.e. $a_n = 2n$) and where $p_n$ is the $n+1$-th prime number, consists of terms $4,6,10, 14, \ldots$.

Challenge (Subsequence of a constant sequence)

Prove that if a sequence $(a_n)$ is constant then any subsequence of it is also constant.

Challenge (Subsequence of an eventually constant sequence)

Prove that if a sequence $(a_n)$ is eventually constant then any subsequence of it is also eventually constant.

Challenge

Can you find a non-eventually-constant sequence with a constant subsequence?

Partial Functions

Let $p \maps \NN \to \NN$ be the function defined by letting $p(n)$ to be the largest prime number less than or equal to $n$.