Lesson (II)
Table of contents
Isomorphisms
An isomorphism between two sets $A$ and $B$ is a pair of functions \[ f \maps A \to B \,\,\, \text{and} \,\,\,\, g \maps B \to A \] such that $g\circ f = \id_A$, and $f\circ g = \id_B$.
In such a situation, we call $f$ an inverse of $g$ and $g$ and inverse of $f$.
We can think of functions $f$ and $g$ above as no data-loss ``processes’’, e.g. conversion of files to different format without data being lost.
The sets $A$ and $B$ are said to be isomorphic in case there exists an isomorphism between them. In this case, we use the notation $A \iso B$. We say sets $A$ and $B$ are uniquely isomorphic if there is a unique pair of mutually inverse functions $f$ and $g$ which witness this isomorphism.
For exmaple, any two singletons are uniquely isomorphic. If we have sets $\set{🥕}$ and $\set{⛄}$ then they are isomorphic since we can find functions $f\maps \set{🥕} \to \set{⛄}$ defined by $f(🥕) = ⛄$ and $g(⛄) = 🥕$. This pair of function is an isomorphism since $f(g(⛄)) = f(🥕) = ⛄$ and $g(f(🥕)) = g(⛄) = 🥕$. Moreover, $f$ and $g$ are uniquely determined.
Isomorphisms are revetible processes and they let us to go back and forth between two different sets without loss of information. In fact, there is a sense in which somorphisms, rather than equality of sets is the correct notion of sameness of sets: For instance in the example of $\set{⛄}$ and $\set{🥕}$ both sets Since all the singletons are isomorphic
Challenge
We also have a function $\set{🥕} \to \set{🥕,⛄}$ which assigns 🥕 to 🥕. Does this function have an inverse? Why not?
Theorem (Inverses are Unique)
An inverse of a function, if it exists, is unique.
Let us give a less trivial exmaple of isomorphism of sets: Previously, we defined the cartesian product $A \times B$ of two sets $A$ and $B$ to consists of all the pairs $(a,b)$ where $a \in A$ and $b \in B$. Now, we show that the order of forming products does not matter, the sets $A\times B$ and $B \times A$ are isomorphic. To show this, we need to construct a pair of inverse functions \[ f\maps A \times B \to B \times A \quad \text{ and } \quad g\maps B\times A \to A\times B \, .\] We define $f$ by the assignemnt $(a,b) \maps (b,a)$ and $g$ by the assignemnt $(b,a) \maps (a,b)$. Now, \[ f \circ g (b,a) = f(a,b) = (b,a) \quad \text{ and } \quad g \circ f (a,b) = g(b,a) = (a,b) \, , \] for all $a \in A$ and $b \in B$. Therefore, by function extensionality, we have $ g\circ f = \id_{A \times B}$, and $f\circ g = \id_{B\times A}$. We conclude that \[ A \times B \iso B \times A \, .\]
Challenge
- Show that for all sets $A$, we have $A \times 1 \iso A$.
- Show that for all sets $A,B,C$ we have $A \times (B \times C) \iso (A\times B) \times C$.
- Show that for all sets $A,B,C$ we have $(A \times B) \times C \iso C \times (B\times A)$.
Challenge (Commutativity and Associativity of Disjoint Unions)
- Show that for all sets $A,B$ we have \[ A + B \iso B + A \, \]
- Show that for all sets $A,B,C$ we have \[ A + (B + C) \iso (A + B) + C \, .\]
Challenge
Is it true for all sets that $1 + A \iso A$? If not, find a condition about $A$ which forces $1 + A \iso A$ to be true.
Weaker Notions
The inverse functions we introduced above are sometimes called two-sided inverses; the reason behind it is clear, it does not matter in which order we compose the functions $f$ and $g$, whether $f$ appears to the right of $g$ or to the left of it, the result is identity. There are however weaker notions of inverse which are quite useful. Here are the two most important ones:
- A retract (aka left inverse) of a function $f \maps A \to B$ is a morphism $r \maps B \to A$ such that $r \circ f = \id_A$. In this case we also say $A$ is a retract of $B$.
- A section (aka right inverse) of function $f \maps A \to B$ is a morphism $s \maps B \to A$ such that $f \circ s = \id_B$.
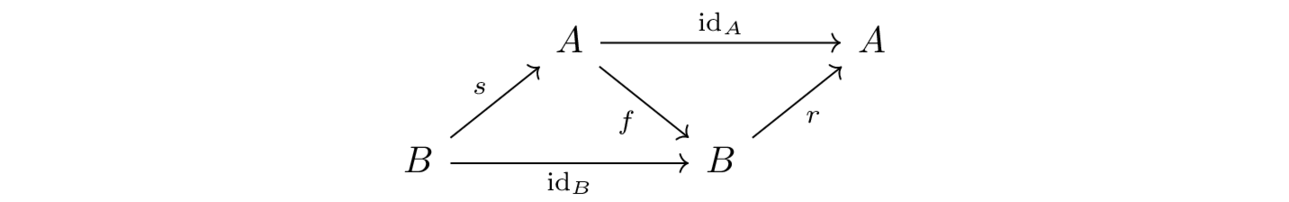
Challenge (Canonical Function From Sum to Union)
There is a canonical function $A + B \to A \cup B$ which takes $(a,0)$ to $a$ and $(b,1)$ to $b$.
- Is this function an isomorphism?
- Does this function have a section?
Bijections
A function $f \maps A \to B$ is injective (also called one-to-one) whenever the following sentence holds. \[ \forall a,b \in A,\, f(a) = f(b) \Rightarrow a=b \] An injective function is said to be an injection.
Theorem (Sections are injective.)
Every function with a retract is injective.
Proof
Suppose $f \maps A \to B$ is function with a retract $r \maps B \to A$. Therefore, $r \circ f = \id_A$. Suppose $f(a) = f(\pr{a})$. It follows that \[ a = \id_A (a) = r \circ f (a) = r (f(a)) = r(f(\pr{a})) = r \circ f (\pr{a}) = \id_A (\pr{a}) = \pr{a} \, .\]
Challenge
Is the converse of the above theorem also true?
Theorem
Let $f \maps A \to B$ be a function. If $f$ is injective and $X$ is inhabited, then $f$ has a retract.
The dual concept to injection is surjection. A function $f \maps X \to Y$ is surjective (aka onto) whenever \[ \forall y \in Y,\ \exists x \in X,\ f(x) = y \] holds. A surjective function is said to be a surjection.
Challenge (Surjectivity and Inhabitedness)
Show that the function $\cons{X} \maps X \to 1$ is surjective if and only if $X$ is inhabited.
Theorem (Retractions are surjective.)
Every function with a section is surjective.
Challenge
Prove that the canonical function $A + B \to A \cup B$ is a surjection.
A function which is both injective and surjective is said to be bijective. An injective function is said to be an bijection.
Theorem
Every isomorphism of sets is a bijection.
Proof
Suppose $f \maps A \to B$ is an isomorphism. Then $f$ has an inverse $g \maps B \to A$. The function $g$ serves both as a section and as a retraction for $f$. Therefore, by theorems above $f$ is both injective and surjective, and hence it is bijective.
Challenge
Does the converse of the last theorem hold as well? If yes, give a proof, and if no, supply a counter-example.
Challenge
Show that if $A$ and $B$ are disjoint sets (i.e. their intersection $A \cap B$ is empty) then the canonical function $A + B \to A \cup B$ is in fact an isomorphism.
Set of Functions
Given two sets $A$ and $B$ we denote the set of functions from $A$ to $B$ by $B^A$. Thus, $f \in B^A$ if and only if $f \maps A \to B$ is a function. Similar to the terminology for numbers, the set $B^A$ is sometimes called “$B$ to the power of $A$” (or the “exponentiation of $A$ to $B$”).
By the definition of functions as functional relations, \[ B^A = \set{R \subseteq A \times B \mid R \text{ is a functional relation} }\] Therefore, $B^A \subseteq \powerset{A \times B}$.
We can reformulate some of the operation on functions, such as composition and evaluations,in terms of functions on the sets of functions.
Theorem (Composition as Function)
The composition operation is a function $\circ \maps B^A \times C^B \to C^A$. If $(f,g) \in B^A \times C^B$ then $f \maps A \to B$ and $g \maps B \to C$ are functions and therefore their composition $g \circ f$ is a function from $A$ to $C$ and hence $g \circ f \in C^A$. What remains to prove is to show that the assignment $(f,g) \mapsto g \circ f$ is well-defined (i.e. it is a total and deterministic assignment). Suppose $(f,g) = (f’,g’)$. We want to show that $g \circ f = g’ \circ f’$. We use function extensionality to prove that. Take an arbitrary $a \in A$. Since $(f,g) = (f’,g’)$, we have $f=f’$ and $g=g’$. We have $g \circ f (a) = g(f(a)) = g(f’(a)) = g’(f’(a)) = g’ \circ f’ (a)$. The first equality in the this chain of equalities holds by the definition of $g \circ f$, the second by our assumption that $f=f’$, the third by by our assumption that $g=g’$, and finally the last equality by the definition of $g’ \circ f’$. Since $a$ was arbitrary, by function extensionality, we conclude that $g \circ f = g’ \circ f’$.
Challenge (Evaluation as Function)
For a function $f \maps A \to B$ and an element $a \in A$, we can evaluate $f$ at $a$ simply by applying $f$ at $a$. Therefore, the result of evaluation of $f$ at $a$ (aka application of $f$ at $a$) is the element $f(a)$ in $B$. Find a function which evaluates a function at an element of its domain.
Theorem (Properties of Function Sets)
Suppose $X, Y, Z$ are sets. We have
- $ X^\emptyset \iso 1 $.
- $\emptyset^X \iso 1 $ if and only if $X = \emptyset$. In particular $\emptyset^\emptyset \iso 1$.
- $X^{Y + Z} \iso X^Y \times X^Z $.
Revisiting Functions of Many Arguments
In section Functions of Many Arguments we observed that a function of many arguments can be obtained by iteration of application of a function of a single argument. Now, we make this observation into a function. As we saw, a function $f \maps X \times Y \to Z$ can be alternatively thought of as $F \maps X \to Z^Y$ (where $F(x)$ is a function from $Y$ to $Z$ taking $y$ to $f(x,y)$). In other words, $f$ and $F$ are interchangeable.
Theorem (Frege-Schönfinkel-Curry)
- For all sets $X,Y,Z$ there is an isomorphism \[ X^{Y \times Z} \iso (X^Y)^Z \ \, \]
Proof
We construct a pair of functions $\mathsf{curry} \maps Z^{X \times Y} \to (Z^Y)^X$ and $\mathsf{uncurry} \maps (Z^Y)^X \to Z^{X \times Y}$ and prove they are inverses of each other. We define them by \[ \mathsf{curry} \, f \defeq \lambda x \, . \lambda y. \, f(x,y) \] and \[ \mathsf{uncurry} \, g \defeq \lambda a \, . (g \pi_1(a)) \pi_2(a) \]
Remark (Currying)
Recall that in the lesson on natural deductions we saw a form of currying for propositions; in Lean it was
theorem curry
(P Q R : Prop) : (P ∧ Q → R) → (P → (Q → R) :=
begin
intro h,
intro hp,
intro hq,
have hpq : P ∧ Q, from and.intro hp hq,
exact h hpq,
end
theorem uncurry
(P Q R : Prop) :
(P → (Q → R)) → (P ∧ Q → R) :=
begin
intro h,
intro hpq,
have h₁, from h hpq.left,
exact h₁ hpq.right,
end
The elegant relationship between logic and set theory gets even more elegant when we discover in section that the currying for propositions and the currying for sets are basically the same thing!
Theorem 5.1 Consider the core theory given by the axioms of extensionality, separation, emptyset, and pair with intuitionistic logic. The axiom of foundation in the form of a minimal ∈-element: ∀x [∃u ∈ x ⇒ ∃y (y ∈ x ∧ ∀z (z ∈ y ⇒ z ∈ x))], implies the law of excluded middle. Moreover, if separation is limited to bounded formulae, excluded middle for bounded formulae can be derived.
Propositions as Sets
Let us denote by $\pf{P}$ the set of proofs a proposition $P$. In set-builder notation \[ \pf{P} = \set{p \mid p \text{ is a proof of } P } \]
For a moment let’s travel back in time and have a recall of propositional connectives here. How soon things escalated!
Recall that
- a proof of a conjunction $P\land Q$ is pair consisting of a proof of $P$ and a proof of $Q$. Therefore, we have \[ \pf{P \land Q } = \pf{P} \times \pf{Q} ]]
- a proof of implication $P \To Q$ gives for every proof of $P$ a proof of $Q$. Therefore $\pf{P \To Q} \subseteq (\pf{P} \to \pf{Q})$ where $\pf{P} \to \pf{Q}$ is the set of functions from $\pf{P}$ to $\pf{Q}$. Also, if we have a function $\pf{P} \to \pf{Q}$ then we have a specification which specifies a proof of $P$ to a proof of $Q$. But, this specification is a proof of $P \To Q$. Altogeher, we have \[ \pf{P \To Q} = (\pf{P} \to \pf{Q}) \]
- a proof of a negation $\neg P$ is
Choice
Choice