Other Classical Principles of Reasoning
Table of contents
- Other Classical Laws
- Maximally Negated Propositional Formulae
- Disjunctive and Conjunctive Normal Forms
Other Classical Laws
LEM and LDN ensure that for every proposition $P$ the propositions $P \vee \neg P$ and $\neg \neg P \To P$ are tautologies of classical propositional logic. In this section we will provide some more classical tautologies and equivalences. Again, for most mathematicians, there are no controversies in using them. We shall see how they can be derived from LEM.
Proofs by Contrapositive
For propositions $P$ and $Q$, we can form the implication $P \To Q$. The proposition $\neg Q \To \neg P$ is known as the contrapositive of $P \To Q$. Every implication constructively implies its contrapositive, that is we can derive $\neg Q \To \neg P$ from $P \To Q$:
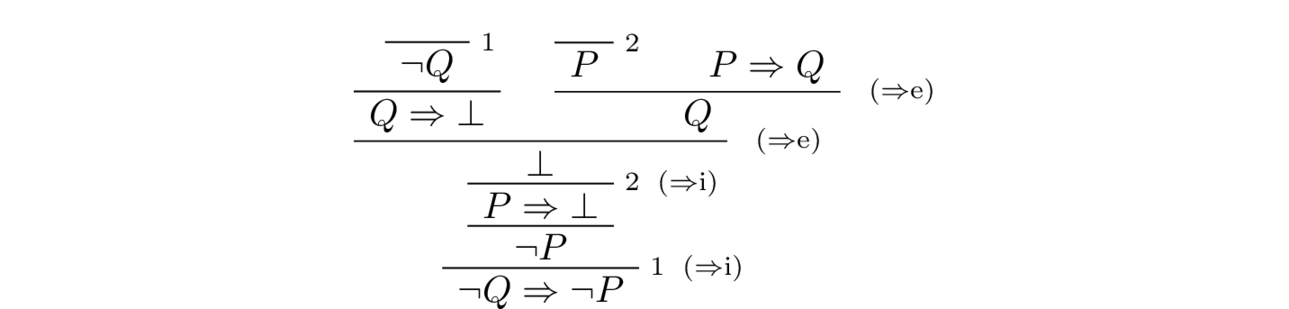
Here we give a proof of this in Lean which uses only the basic tactics intro and exact:
example: (P → Q) → (¬ Q → ¬P) :=
begin
intro hpq,
intro nq,
intro hp,
exact nq (hpq hp),
end
Intuitively, this can be justified as follows: we know that whenever $P$ is the case so is $Q$. Now, if we also know that $Q$ is not the case then we must conclude that $P$ is not the case since otherwise $P$ is the case and hence $Q$ is the case. Therefore, both $Q$ and $\neg Q$ are the case which cannot be the case.
Now, if we allow ourselves to turn on the classical reasoning engine, we can in fact prove the converse of the above implication, that is $\neg Q \To \neg P$ implies $P \To Q$. A proof of $P \To Q$ from a proof of $\neg Q \To \neg P$ is called proof by contrapositive. Here is a proof of it in natural deduction using the Law of Double Negation.
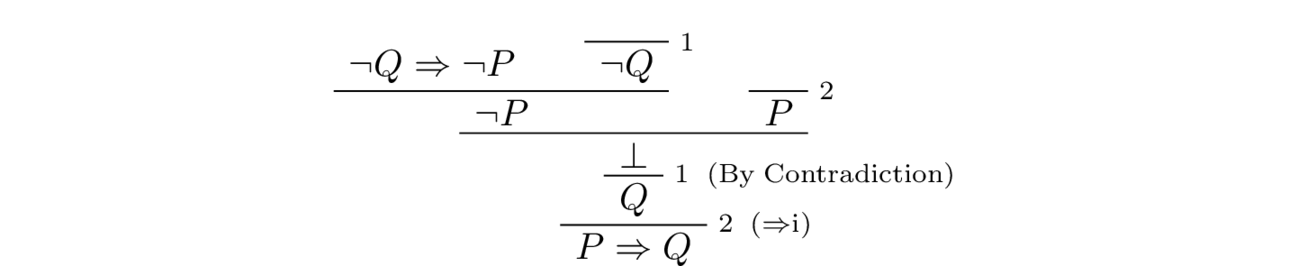
and here is the lean proof:
open classical
variables (P Q : Prop)
example (h : ¬ Q → ¬ P) : P → Q :=
assume hp : P,
show Q, from
by_contradiction
(assume hnq : ¬ Q,
have hnp : ¬ P, from h hnq,
show false, from hnp hp)
Heed the need for open classical to tell Lean that we decided to use classical reasoning (proof by contradiction).
Classical reasoning, therefore, proves that $P \To Q$ and its contrapositive $\neg Q \To \neg P$ are equivalent, i.e. \[ P \To Q \iff \neg Q \To \neg P \] is a tautology.
✏️ Challenge
What error does Lean give you if you forget to include open classical in your code?
De Morgan’s Laws
In propositional logic and Boolean algebra, De Morgan’s laws are a pair of transformation rules that are valid classical rules of inference. In classical logic, these rules allow the expression of conjunctions in terms of disjunctions and vice versa using the logical operation of negation.
Although these rules are named after Augustus De Morgan, a 19th-century British mathematician, they were known to Aristotle and again in the 14th century, to William of Ockham. The algebraic formulation of these laws which De Morgan discovered was under the enormously successful program of algebraization of logic initiated by Boole.1
In one direction De Morgan laws say that for all propositions $P$ and $Q$ we can prove the following propositions
\[ \neg P \lor \neg Q \To \neg (P \land Q) \] \[ \neg P \land \neg Q \iff \neg (P \lor Q) \]
Here we give a Lean proof of the above propositions:
example : ¬ P ∨ ¬ Q → ¬ (P ∧ Q) :=
begin
intro hnpq,
cases hnpq,
{intro hpq,
have hp, from and.left hpq,
have this, from hnpq hp,
exact this,
},
{
intro hpq,
have hq, from and.right hpq,
have this, from hnpq hq,
exact this,
},
end
✏️ Challenge
Can you find out the natural deduction proof of these Lean proofs?
We note the asymmetry in the rules above; we are missing one implication. Indeed the proposition
\[ \neg (P \land Q) \To \neg P \lor \neg Q \]
is not constructively valid and we could not have constructed a proof of it using the intuitionistic rules of natural deduction.
✏️ Challenge
Give a natural deduction proof of $\neg (P \land Q) \To \neg P \lor \neg Q$ and translate it to Lean.
Classically, an implication is equivalent to a disjunction
For propositions $P$ and $Q$, we can show constructively that $\neg P \lor Q \To P \To Q$ is a tautology. We first give a Lean proof of this:
example: ¬ P ∨ Q → P → Q :=
begin
intro hpq,
intro hp,
cases hpq,
{ exfalso,
have this,
from hpq hp,
exact this,
},
{
exact hpq,
},
end
✏️ Challenge
Can you write down the natural deduction proof of this Lean proof?
If we admit the use of classical reasoning, we can prove the converse implication as well and therefore, we can show that the propositions $P \To Q$ and $\neg P \lor Q$ are (classically) equivalent.
In the 19th century, Boole, De Morgan, and others brought about a first step toward reform to Aristotelian logic which surprisingly until then remained more or less the same as it was in Aristotle’s Prior Analytics. However, in the end the work of Boole and others amounted only to a clarification of Aristotelian logic with the machinery of algebra (the so-called the Boolean Algebra). The real reform of Aristotelian logic happens with the efforts of the German philosopher and logician Gottlob Frege in his work Begriffsschrift. Frege maintains that his logic differs from Boole’s in basic design: “This is due to the fact that I have moved further away from Aristotelian logic. For in Aristotle just as in Boole the formation of concepts through abstraction is the fundamental logical operation and judging and inferring are brought about through direct or indirect comparison of the extension of these concepts.” ↩
Maximally Negated Propositional Formulae
Recall that if we assume LEM then the De Morgan laws say that for all propositions $P$ and $Q$ we can prove the following propositions
\[ \neg (P \land Q) \iff \neg P \lor \neg Q \] \[ \neg (P \lor Q) \iff \neg P \land \neg Q \]
Also, classically we have
\[ \neg P \lor Q \iff P \To Q \]
which implies
\[ \neg (P \To Q) \iff P \land \neg Q \; . \]
Finally,
\[ \neg\neg P \iff P \]
by the Law of Double Negation. Using these equivalences, it looks like we can always push negations down to atomic propositions. For example, we have
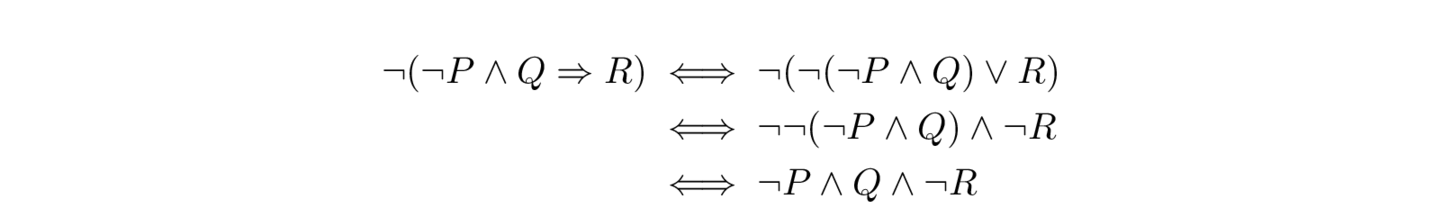
A propositional formula is maximally negated if the only instances of the negation operator $\neg$ appear immediately before an atomic proposition (propositions involving no logical operators in their formation).
✏️ Challenge
Translate the condition of being maximally negated for propositional formulae to a condition for their parsing trees.
Theorem Every propositional formula is logically equivalent to a maximally negated formula.
✏️ Challenge
Give a precise proof of this theorem.
Disjunctive and Conjunctive Normal Forms
Disjunctive normal forms
Let $P,Q,R$ be propositional atoms. Consider the propositional formula
\[ P \To (Q \land R) \]
Classically, this formula is equivalent to
\[ \neg P \lor (Q \land R) \]
By distributivity of $\lor$ over $\land$, we obtain the following equivalent formula
\[ (\neg P \lor Q) \land (\neg P \lor R) \]
We say a propositional formula is a Conjunctive Normal Form (CNF) if it is a conjunction of disjunctions of (possibly negated) propositional atoms (aka propositional variables, literals). This means a formula is in conjunctive normal form if it has the form $A_1 \land · · · \land A_m$ , where each $A_i$ is a disjunctions of (possibly negated) propositional atoms.
✏️ Exercise
Suppose $P$, $Q$, and $R$ are propositional formulas. Which of the following formulas are CNF?
- $P \land Q$
- $(P \lor \neg Q \land R)$
- $\neg P$
- $\neg P \land \neg Q$
- $(P \lor Q \To Q )$
We say that a propositional formula $B$ is a CNF of a propositional formula $A$ if $B$ is equivalent to $A$ and $B$ is a CNF. For instance the proposition $(\neg P \lor Q) \land (\neg P \lor R)$ is a CNF of propositional formula $P \to (Q \land R)$.
At first sight it might seem very restrictive to only work with CNFs. However, in classical logic, the following theorem tells CNFs are enough!
Theorem. For every propositional formula $A$, there is an equivalent proposition $B$ which is in conjunctive normal form.
We need more tools to give a complete proof of this theorem; we give a full proof of it in the lesson on induction. For now, we describe an algorithm to compute the conjunctive normal from of any given formula. However, to prove that this is the correct algorithm for any input we need to use induction on the height of formulae.
Here are steps in computing the conjunctive normal form.
Eliminate $\iff$ and $\To$ by repeatedly applying the following (classical) equivalences: \[ (A \iff B) \iff ((A \To B) \land (B \To A)) \] \[ (A \To B) \iff (\neg A ∨ B) \]
Push negations in until they appear in front of atoms only by repeatedly using the equivalences \[ ¬¬A \iff A \] \[ ¬(A ∧ B) \iff ¬A ∨ ¬B \] \[ ¬(A ∨ B) \iff ¬A ∧ ¬B \]
And finally, to obtain CNF, push disjunctions in until they apply only to atoms by repeatedly using the equivalences \[ A ∨ (B ∧ C) \iff (A ∨ B) ∧ (A ∨ C) \]
Of course since disjunction is commutative we can also use $(B ∧ C) ∨ A \iff (B ∨ A) ∧ (C ∨ A)$.
disjunctions of (possibly negated) propositional atoms
Not only does the theorem above not hold intuitionistically, it is also not pragmatic in certain cases: sometimes converting to CNF results in an exponential blow up in formula size! For instance if we have $\iff$: