Link Search Menu Expand Document
Introduction to Proofs

Homework (II)

Problem 1. Show that the law of double negation holds constructively for negative propositions, i.e. $A \iff \neg \neg A$ whenever $A$ is a propositional formula of the from $\neg P$.

  1. Write a natural deduction proof.
  2. Write a Lean proof.

Problem 2. Here is a proof of $\neg (P \iff \neg P)$ using the Law of Excluded Middle.

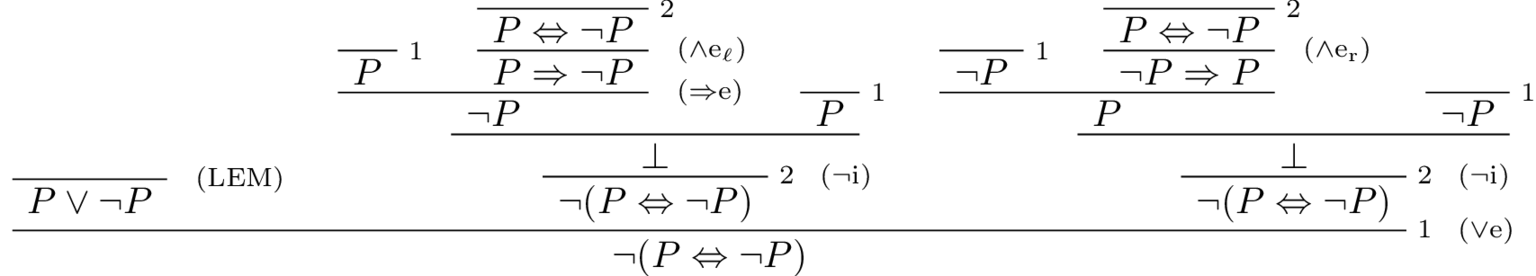
contradiction_implication_classical

Is it possible to prove $\neg (P \iff \neg P)$ constructively (i.e. without using classical logic)? If so, construct such a proof. If no, give your reason and/or intuition why you think a constructive proof is not possible.

Problem 3. Using classical reasoning, show that for all propositions $P$ and $Q$ the following formulae are tautologies:

  1. $P \lor (P\To Q)$
  2. $(P \To Q) \lor (Q \To P)$

Problem 4. In this exercise we’ll learn about Peirce’s law, a curiosity of classical logic. Let $P$, $Q$ and $R$ be propositions.

  1. With the help of the law of double negation construct a proof of proposition \[ ((P \Rightarrow Q) \Rightarrow P) \Rightarrow P \] in the style of natural deduction.
  2. Write this proof in Lean.

Problem 5. An integer $m$ is said to divide an integer $n$, written $m \mid n$, if there exists an integer $k$ such that $n = mk$. We write $m \nmid n$ for $\neg (m \mid n)$. With this definition in hand, decide whether the following proof that $3 \nmid 20$ is constructive or not? Justify your answer.

Proof. Assume to the contrary that $3 \mid 20$. Then there exists a $k$ such that $20 = 3k$. By the fundamental theorem of arithmetic, $k$ has some unique prime factorization $k = 3 \prod_{i=1}^{n} p_i$. So $20$ factors into primes as $20 = 3 \prod_{i=1}^{n} p_i$. But we also know that $20 = 2 \times 2 \times 5$. The existence of two distinct prime factorizations for $20$ contradicts the uniqueness guaranteed by the fundamental theorem of arithmetic. We thus conclude that $3 \nmid 20$.

Problem 6. Give a constructive proof of the fact that the multiplication of two non-zero rational numbers is non-zero.

Tips & Hints

  • For problem 6, you might want to use the fact that a non-zero rational number has a multiplicative inverse.