Deconstrucing Propositional Formulae
Table of contents
Outline
In this lesson we shall investigate the structural properties of intuitionistic propositional calculus we introduced in the previous lesson.
Parsing trees (sometimes called formation trees) are a useful device to display the data of a propositional formula in a tree where the leaves of the tree are populated by the atomic propositions and other nodes are populated by connectives. Parsing trees give us an easier way to detect all the subformulae of a propositional formula visually.
Analysing Propositional Formulae and Subformulae
Well-formed Propositional Formulae
We used connectives to build from atomic propositions compound propositions which we called propositional formulas. For instance if $P$ and $Q$ are atomic propositions then $P \land Q$ is a propositional formula which is not atomic anymore. Note, however, not any list of characters involving atomic propositions and connectives yields a propositional formula. There are certain combination which we simply cannot accept as a propositional formula; for instance neither of the expressions
- $ P \land Q \neg $,
- $ \neg P \, Q$,
- $\To P$,
- $ P \land Q R $
is a propositional formula. To remedy this problem, we say that a propositional formula $A$ is well-formed if it is either atomic, or it can be obtained by using the construction rules below:- If $A$ is well-formed, then so is $\neg A$.
- If $A$ is well-formed, then so is $(A)$.
- $A$ and $B$ are well-formed then so are $A \To B$, $A \land B$, $A \lor B$, and $A \iff B$.
Clearly we are defining the notion of well-formedness in terms of well-formedness! For instance we said $\neg A$ is well-formed if $A$ is well-formed, but how do we judge that $A$ is well-formed? Isn’t this definition self-referential and therefore, and invalid definition? Not really, this definition is in fact recursive (More on recursive definitions on future lessons): Consider for instance the formula $(P \land Q) \lor R$. We argue that this formula is well-formed by rule 3 and since
- $R$ is well-formed since it is atomic,
- $(P \land Q)$ is well-formed by rule 2 and since
- $P \land Q$ is well-formed by rule 3 and since
- $P$ is well-formed since $P$ is atomic.
- $Q$ is well-formed since $Q$ is atomic.
- $P \land Q$ is well-formed by rule 3 and since
What we have here is a recursive argument establishing that $(P \land Q) \lor R$ is well-formed. The proof is constructed from top to bottom, but should be read from bottom to up: since $P$ and $Q$ are atomic they are well-formed, and therefore, by rule 3, the conjunction $P \land Q$ is well-formed. Hence, by rule 2, $(P \land Q)$ is well-formed. The atomic proposition $R$ is well-founded, and therefore, by rule 3, the disjunction $(P \land Q) \lor R$ is again well-founded.
Unique Readability
Recall that we assigned meanings to propositional formulas (the meaning of a proposition is determined by what counts as a verification/witness/proof of it). For instance the meaning of $P \land Q$ is given by the collection of all pairs of proofs, one for $P$ and and one for $Q$. But in order to assign meaning to the expression (i.e. syntax) of a (would-be) proposition, we have to read off that expression as a unique proposition. In what follows, we shall give a detailed example.
Suppose we are given an expression like
\[ P \lor Q \land \neg P \To Q \]
Note that since we are not assigning any meaning to the expressions above, they are just a list of characters:
["P","∨","Q","∧","¬","P","→","Q"]
It is not clear how to read it since it can be read in more than one way; Different bracketing of list of symbol characters above results in (possibly) distinct readings of the expression $P \lor Q \land \neg P \To Q$, some of which are gathered in below:
- $(P \lor (Q \land \neg P)) \To Q$,
- $(P \lor Q) \land (\neg P \To Q)$,
- $((P \lor Q) \land (\neg P)) \To Q$. Can you find more ways to read this expression?
Now that we have added brackets (in different ways) to our original expression, the corresponding lists become larger:
["(","P","∨","(","Q","∧","¬","P",")",")","→","Q"]["(","P","∨","Q",")","∧","(","¬","P","→","Q",")"]["(","(","P","∨","Q",")","∧","(","¬","P",")",")","→","Q"]
Note that in the first two cases we have two “(” and two “)” and in the last case we have three “(” and three “)”.
Now that we have decided in three (but possibly more!) different ways how the expression ["P","∨","Q","∧","¬","P","→","Q"] can be read, we note that it is only the last reading which is a tautology, and here is a proof of it:
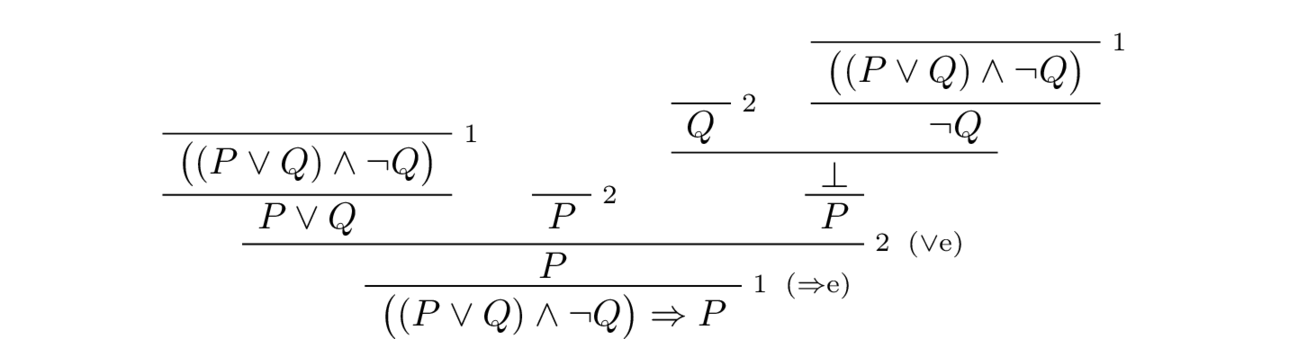
The problem explicated here is akin to the ambiguity of the arithmetic expressions $3 + 2 \times 2$: Is it supposed to be parsed as $(3 + 2) \times 2$ or rather $3 + (2 \times 2)$? Our solution to the readability problem above for the propositions is similar to the solution we know to solve parse arithmetic expressions $3 + 2 \times 2$, namely convention.
Binding Priorities
When writing expressions in symbolic logic, logicians adopt a conventional order of reading of operations which allows them to drop superfluous parentheses. When parsing an expression consisting of propositional variables and connectives the following conventions are followed:
- Negation binds most tightly.
- Then, conjunctions ($\land$) and disjunctions ($\lor$) bind from right to left.
- Finally, implications ($\To$) and bi-implications ($\iff$) bind from right to left.
So, for example, according to the last convention, the expression $P \To Q \To R$ is read as $P \To (Q \To R)$ and according to the conventions 1,2, and 3 the expression $\neg P \lor Q \To R \land S$ is read as $((\neg P) \lor Q) \To (R \land S)$.
It is interesting to see the effect of these conventions at the raw level of list of characters: The expression $\neg P \lor Q \To R \land S$ can be rendered as the list ["¬", "P","∨","→", "R", "∧", "S"] and after inserting the brackets it is rendered as ["(", "(", "¬", "P", ")", "∨", "Q", ")", "→", "(", "R", "∧", "S", ")"].
The operation of following the binding conventions to read list of logical symbols is called parsing.
Remark
- The second convention does not state the either of $\land$ or $\lor$ has priority in binding over the other, and therefore, if necessary, we need to insert few more brackets to eradicate ambiguity. For instance $P \lor Q \land R$ can be read in two different ways. So, if one means to express the idea of taking the disjunction of $P$ and $Q$ first and take the conjunction of the resulting formula with $R$ one has to insert two more brackets as follows: $ (P \lor Q ) \land R$.
- Although the conventions consistently say that we should read the operators from right to left, sometimes if we read from the left to right, we get due to the associativity laws we proved before. Therefore, if we write for example $P \land Q \land R$ it is not ambiguous since both readings result in the same proposition.
Subformulae
All fundamental methods in logic are based on analyzing formulas in terms of their subformulas. Subformulas are defined recursively:
| Formula | Subformula |
|---|---|
| $A \To B$ | $A \To B$ together with the subformulae of $A$ and the subformulae of $B$ |
| $A \land B$ | $A \land B$, together with the subformulae of $A$ and the subformulae of $B$ |
| $A \lor B$ | $A \lor B$ together with the subformulae of $A$ and the subformulae of $B$ |
| $\neg A$ | $\neg A$ together with the subformulae of $A$ |
For example, the subformulae of $P \lor \neg Q \To (\neg S \land T)$ are
- $P \lor \neg Q \To (\neg S \land T)$
- $P \lor \neg Q$
- $(\neg S \land T)$
- $P$
- $\neg Q$
- $\neg S$
- $T$
- $Q$
- $S$
✏️ Challenge
How do you detect all of the subformulae of a propositional formulas from its parsing tree?
✏️ Challenge
- Write an informal algorithm which
- takes a propositional formula as an input, and
- outputs its parsing tree and all of its subformulae.
- Write the informal algorithm of the previous part as a program in your favourite programming language (e.g. Java, Python, Haskell, OCaml, Lean, etc).
Parsing trees
Suppose we are given the following expression
\[ (P \To Q \To R) \To P \land Q \To R \]
By the binding conventions above, we insert the brackets as follows:
\[ (P \To (Q \To R)) \To (P \land Q) \To R \]
The parsing tree corresponding to this bracketing is drawn in below:
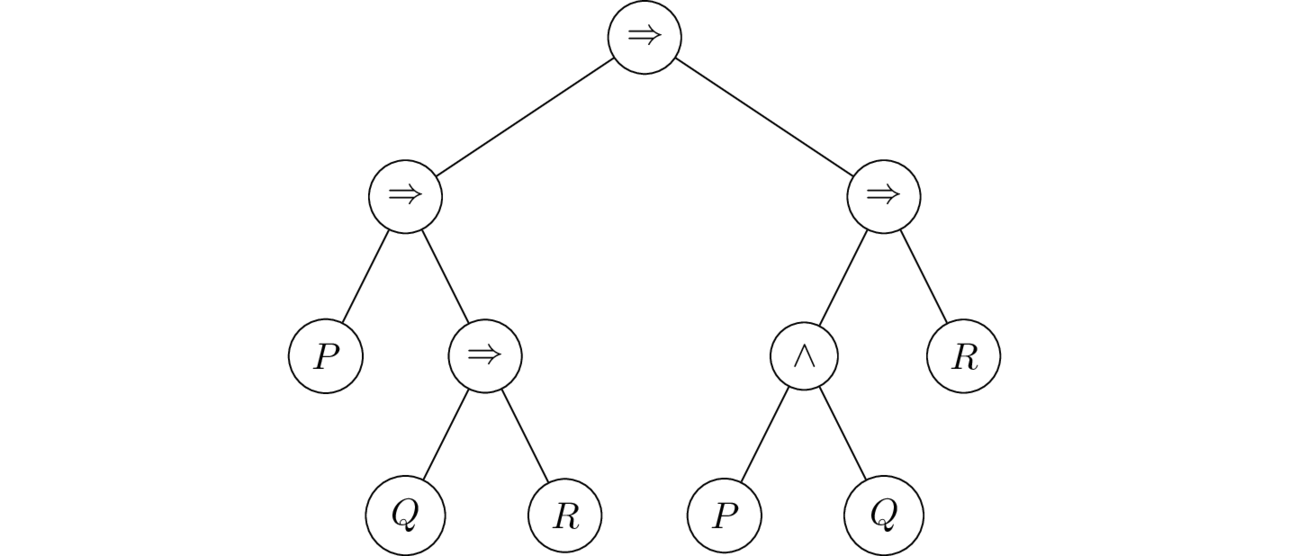
Here is the .tex code (using the package tikzpicture) which generates the parsing tree above:
\begin{tikzpicture}[nodes={draw, circle}]
\node{$\To$}
child { node {$\To$}
child { node {$P$} }
child { node {$\To$}
child{ node {$Q$} }
child{ node {$R$} }
}
}
child [missing]
child [missing]
child {node {$\To$}
child { node {$\land$}
child { node {$P$}}
child { node {$Q$}}
}
child { node {$R$} }
};
\end{tikzpicture}
One thing to note is that the tree above is a binary tree, that is every node has two branches. This is due to the fact that the connectives $\To$, $\land$, $\lor$ and take two inputs and spit out one output.
But what about negation connective which takes only takes one input? Well, you might recall from previous lesson that we established for every proposition $P$ the propositional formulae $\neg P$ and $P \To \bot$ are the same as they have exactly the same introduction and elimination rules). Therefore for any proposition $P$ we shall display the parsing tree of $\neg P$ as follows:

✏️ Exercise
Draw the parsing tree for the following propositional formulae
- $P \land (P \To Q) \To P \land Q$
- $ \neg P \lor Q \To P \To Q $
- $\neg (P \land Q) \To \neg P \lor \neg Q$
Sequents from natural deduction proofs
Sometimes we are interested in compressing the content of our natural deduction proofs and present to our readers only the assumptions and the conclusion(s). There is a systematic way to do this and it is known as the sequent calculus.
Suppose, starting from proposition formulas $A$ and $B$ we have concluded another propositional formula $C$ in some way. For example one such way is illustrated in below where the vertical dots indicate valid inferences hidden from public view for some reason.
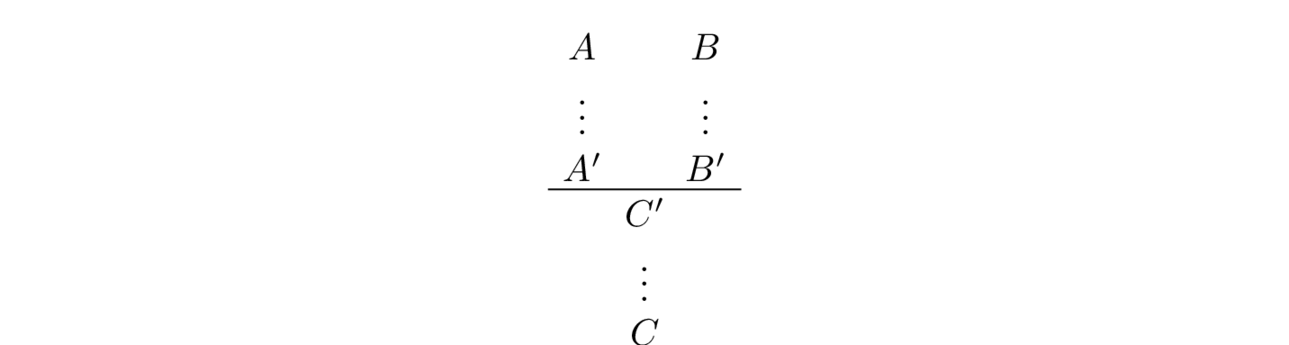
All we know is that from $A$ it is possible to derive $\pr{A}$, from $B$ possible to derive $\pr{B}$ and from $B$ and $\pr{B}$ possible derive $\pr{C}$, and from $\pr{C}$ it is possible to derive $C$.
We can implement this data available to us using sequents:
$A \vdash \pr{A}$
$B \vdash \pr{B}$
$\pr{A} , \pr{B} \vdash \pr{C}$
$\pr{C} \vdash C$
Here the symbol “$\vdash$” is called “turnstile” and it denotes a derivation from some assumptions, which appear on the left of $\vdash$ to the conclusion(s) which appear on the right of $\vdash$.
Now, suppose after receiving the data above, we pass it on to some other receiver but this time we hide even more information (say, for the reasons of privacy we do not want $\pr{A}$, $\pr{B}$, and $\pr{C}$ to be exposed) so that our receiver can only see the starting assumptions $A$ and $B$ and the final conclusion $C$. Therefore, we pass on the following string of symbols:
$A,B \vdash C$
What we did was to forget the inner structure of the proof above and only remember its periphery. It’s a bit like you click a put a coin on some vending machine to buy some coffee; you really interact with the coin and – if the machine works– coffee. The inner algorithm of the vending machine takes care of the rest Similarly, the sequent $A,B \vdash C$ has less information than the natural deduction proof which gave rise to it.
Now, can we make a system of rules for calculating with sequents like, reflecting the fact that they somehow arose from natural deduction proofs.
Since on the left of $\vdash$ there could be multiple propositional formulas, we would like to have a notation for it: We write
$\Gamma \vdash \alpha$
to indicate that $\Gamma$ is a list of formulas, and $A$ follows from $\Gamma$. For example, in case where
$ A, B \vdash C$
we have $\Gamma = (A,B)$ and the conclusion $\alpha$ is just $C$.
It is possible to have many conclusions such as
$A\land B \vdash A,B$.
$\Gamma, P \vdash P , \Delta$
The first rule we would like to introduce is that