From Propositions To Predicates
Table of contents
Introduction
First-order logic has variables ranging over “individuals”, but not over functions or predicates; such variables are found in second- or higher-order logic.
Predicates
Basically, predicates are propositions which vary! Suppose we want to express the idea of listing propositions
“$2$ is even”,
“$4$ is even”,
“$6$ is even”, etc.
This is an impossible task to do in finite time. We cannot write infinite sentences in finite time/memory. Note that the information specified above is incomplete, nevertheless we got the idea since we understood the pattern: the next sentence in the list will be “$8$ is even”.
But suppose we wanted to explain this to a computer or a Martian instead. Perhaps they do not share the same pattern recognition skills embedded in our language and communication. Our first idea might be to consider the conjunction of all the propositions above:
“$2$ is even” $\land$ “$4$ is even” $\land$ “$6$ is even” $\land$ …
But note that the conjunction connective only applies to finitely many propositions, and we do not have any rules for introducing/eliminating proofs of infinite conjunction. Here’s where predicates come in handy. Simply put, a predicate is a variable proposition: it has a domain of variation $X$ and for each term $x$ of domain $X$ it expresses a proposition $P(x)$. For instance, let $P$ be the predicate with the domain $\mathbb{N}$ of natural numbers and let $P(n)$ to be the proosition “$n$ is even”. Therefore, the list above becomes
P(2), P(4), P(6), etc.
But note that this list only captures a finite initial fragment of $P$. We use the notation $P: \mathbb{N} \to \mathbb{P}\text{rop}$. Here $\mathbb{N}$ is the domain of predicate $P$ and $\mathbb{P}\text{rop}$, the collection of all propositions, indicates that for each natural number $n$, that is a term $n$ of $\mathbb{N}$, the term $P(n)$ is a proposition.
Another limitation of propositional logic which is overcome when we pass to the predicate is to formally express quantified sentences. For instance, the following sentences are not expressible in propositional logic since they include quantifiers “no”, “some”:
- “No child is older than his or her parents.”
- “If someone is alone, they are not with someone else.”
Sometimes the quantification is implicit like in the sentence below:
- “Usain Bolt is the fastest human runner in the world”.
As examples of quantified sentences in mathematics consider the following sentences about natural numbers:
- A natural number is even if and only if it is divisible by two.
- A natural number $n$ is odd if and only if $n+1$ is even.
- Every natural number is even or odd, but not both.
- If some natural number, $n$, is even, then so is $n^2$.
- Any prime number that is greater than $2$ is odd.
- For any three natural numbers $k$, $m$, and $n$, if $k$ divides $m$ and $m$ divides $n$, then $k$ divides $n$.
Variables
As the examples above indicate, we need to find a way to talk about (arbitrary) individuals/objects of certain domains, e.g. $m$, $n$, etc of natural numbers in above. This we achieve by introducing the concept of a variable. For instance a variable $n$ of natural numbers is an unspecified/hypothetical natural number.
Variables are understood in contrast to constants. The values of constants are fixed and is not changing. They have a definite place in the structure of the domains we consider. Some exmaples of constants are $0$ of natural numbers, $\pi$ of the real numbers, and $i$ of the complex numbers.
A simple example of use of variables is as follows: Suppose you want to prove there is no greatest natural number. One way is to list them like $1,2,3, \ldots$ and show that this list is endless. But the problem with this strategy is that however long our list is it is still finite, say up to 1000005673, and does not cover all natural numbers. In other words, we have not shown that literally for every natural number there is a greater one since we have not yet shown this fact for 1000006672. Here is where our reasoning can use the help of variables: Suppose $n$ is the greatest natural number. We know that $n+1$ is greater than $n$. Therefore, $n$ cannot be the greatest natural number.
Note that in the simple proof above we do not know what the value of $n$ is; All we showed was that the assumption of existence of any $n$ with the property of being the greatest natural number leads to a contradiction.
Terms
Starting from variables, we can build complex expressions. Starting with the variables and constants, we can use the function symbols to build up compound expressions like these:
- $ e^x $
- $ \sqrt{3}/4 a^2$
- $x - (y - z)$
- $(x + 1) \times y \times y$
- $(x + y \times z)^2$
Such expressions are called terms. Intuitively, they name objects (constructed from constants and variables) in the intended domain of discourse.
Contexts
We say that a variable is typed if the domain of the variable is made explicit. For instance in the sentence “A natural number $n$ is odd if and only if $n+1$ is even.” the variable $n$ is typed but the variable $x$ in the sentence “$cos^2 x + sin^2 x = 1$” is not.
We denote a typed variable $x$ with a domain $X$ by $x : X$. For instance, in above $n : \mathbb{N}$. For instance $x : \mathbb{R}$ denotes that $x$ is a real-valued variable, while $n : \mathbb{Z}$ denotes that $n$ is an integer variable.
We say that a term is typed whenever all the constants and variables it is comprised of are typed.
A context is a sequence of typed terms. A simple example of a context is the sequence $(n : \NN)$ which has one term only, namely $n : \NN$. In general (i.e. the empty context $()$) the sentence $n + 0 = n$ is not meaningful (because what is $n$?) but in the context $(n: \NN)$ it is, and in fact can be proved. The sentence $1+0 = 1$ is meaningful and true in both the empty context and in the context $n : \NN$ (It does not hurt to have more information in the context, because we can always forget about them). However, the sentence $n + m = m + n $ is meaningless in the context $(n : \NN)$ since the context does not provide enough information what $m$ is.
A more involved example of a context is $(p : \mathbb{P}, n : \mathbb{N}, x : \mathbb{Z} )$ where the variable $p$ is a prime number, the variable $n$ is a natural number, and the variable $x$ is an integer. Only in this context, the following sentence in meaningful:
“$x^n - 1$ is divisible by $p$.”
In fact, this example shows that it is possible to have a predicate over multiple domains: Here the predicate is $P(p,n,x) =$ “$x^n - 1$ is divisible by $p$”. Of course this does not mean that all the values of $P(p,n,x)$ are true; for instance, $P(2,1,3)$ is a true propositions whereas $P(3,1,3)$ is a false propositions.
Another example of context is $(p : \mathbb{Z}, q: \mathbb{Z^+})$ where $\mathbb{Z^+}$ is the domain of all positive integers (hence $0$ is not included in $\mathbb{Z^+}$). In this context, it is meaningful to state that $p/q$ is a rational number.
Substitution of predicates
Suppose we have a variable $x : X$ and an expression $t(x) : Y$, constructed from $x$, and a predicate on $Y$, i.e., an expression $P(y)$ which tells us whether any given $y \in Y$ has a given property. Then we can define a new predicate $Q(x)$ on $X$ by $Q(x) \equiv P(t(x))$.
We substituted the term $t(x)$ for $y$ in the expression $P(y)$. The operation of substitution is ubiquitous in mathematics. For example, whenever we say something like “$2^x + 1$ is odd”, we have substituted the expression $2^x + 1$ for $y$ in the predicate $P(y) = \exists z . y = 2 z + 1$, where all variables range over natural numbers. Here is a simple application of substitution: suppose we want to prove that for all $x \geq 1$, the value of $\ln x$ is positive. Substituting $e^t$, where $t \geq 0$, for $x$ in $\ln x$ we get $\ln e^t = t \geq 0$. Since $e^{(-)}$ is an increasing function of the real numbers, we have $e^t \geq e^0 = 1$. We conclude that $\ln x$ is positive for all $x \geq 1$.
Dependent predicates
Consider the following collection $U$ of colored shapes.

Let us denote the predicates $B$ for “blueness”, $T$ of “being a triangle”, and $E$ for the property of “being equilateral”.
Note that $E$ depends on $T$ in that the property $E$ only applies to triangles. In other words, $T$ is defined only for individuals $x$ such that $T(x)$. This means that the domain of $E$ consists of all individuals $x$ such that $T(x)$ holds. Let’s write ${ T }$ for the domain consisting of all individuals $x$ such that $T(x)$. Therefore $E : { T } \to \props$.
Note that the expression $E(x)$ for an arbitrary $x : U$ does not make sense; what does it mean for a circle to be equilateral? Simply put, $E$ does not apply to $x = \texttt{circle}$.
However, we can extend $E$ to another predicate whose domain is all of $U$, and it agrees with $E$ on ${T}$. Let’s denote this predicate by $E \mid T$. Therefore, $(E \mid T) (x) $ holds if and only if $T(x)$ holds and $E(x)$ holds. Therefore $(E \mid T) (\texttt{circle})$ is false.
Consider the sentence
“If a triangle is blue, then it is equilateral”.
We can write this more formally as \[ T(x) \land B(x) \To (E\mid T) (x) \] which is equivalent to \[ T(x) \To B(x) \To (E\mid T) (x) \]
Here is another example of dependent predicates: We formalize the following invalid argument:
Ulrich is a brilliant mathematician and a gymnast. Therefore, Ulrich is a brilliant gymnast.
Let’s define the predicates
- $M(x) = x \text{ is a mathematician.}$
- $G(y) = y \text{ is a gymnast.}$
- $B_1(z) = z \text{ is a brilliant mathematician.}$
- $B_2(z) = z \text{ is a brilliant gymnast.}$
And let’s denote “Ulrich” with the constant $u$.
Obviously, $\forall x \; B_1 (x) \To M(x)$, and $\forall x \; B_2 (x) \To G(x)$. Alternatively we can consider $B_2$ as a predicate over $M$, that is $B_1 \maps \set{M} \to \props$. Similarly, $B_2 \maps \set{G} \to \props$. Now, the assumption of the argument above gets logicized as \[ M(u) \land G(u) \land B_1 (u) \] and the conclusion as \[ G(u) \land B_2 (u) \, .\] There is no reason that $B_2(u)$ should follow from $M(u) \land G(u) \land B_1 (u)$ since being brilliant as a mathematician and being brilliant as a gymnast are two different things. However, it can still be true that Ulrich is a brilliant gymnast!
Contrast the last example with the following example which is a valid argument:
Human is a featherless biped and an omnivore. Therefore, human is a featherless omnivore. This is because the predicate of “featherlessness” has the same meaning in both “featherless biped” and “featherless omnivore”.
Equality
Equality is fundamental to mathematics, but so far in our treatment of propositional logic and predicate logic we have not talked about equality; this has been a deliberate choice. The equality symbol $=$ is meant to formalize what we mean when we say “something is something else” (e.g. “ascorbic acid is vitamin C” or “5+7=12” ). We are asserting that two different descriptions refer to the same object. Since the notion of equality is very general and can be applied to virtually any domain of discourse, it is falling under the purview of logic.
Equality on (a domain $A$) is a special kind of predicate. Let’s write $Eq(a,b)$ for the proposition $a = b$ in $A$. Axiomatically, we assume that equality predicate $Eq$ satisfies the following three properties:
- reflexivity: $Eq(a,a)$, for any term $a$.
- symmetry: if $Eq(a,b)$, then $Eq(b,a)$.
- transitivity: if $Eq(a,b)$ and $Eq(b,c)$, then $Eq(a,c)$.
However, this is not all we expect from equality; this is too weak to make the predicate $Eq$ into equality ($=$). For instance the predicate $P$ defined by \[ P(\ell, \pr{\ell}) = \ell \text{ and } \pr{\ell} \text{ are parallel lines.} \]
satisfies all the axioms above but we do not want to make the assertion that two parallel lines are identical!
If two terms denote the same thing, then we should be able to substitute one for any other in any expression. Let’s say $e$ is an expression containing $a$ somewhere in it: \[ e = \cdots a \cdots \] If $a=\pr{a}$ then we should be able to replace $a$ with $\pr{a}$ in $e$ and get the same expression, that is the expression \[ \pr{e} = \cdots \pr{a} \cdots \] should be equal to $e$.
Equality requires the same story to be true for substituting equal terms in predicates too; If $a$ and $b$ are two objects which are equal then any property $P$ which holds of $a$ must hold of $b$ and vice versa. That is $a=b$ implies that $P(a) \iff P(b)$ for all predicates $P$. We call this the substitution rule for equality.
We can write the rules for equality in the style of natural deduction:
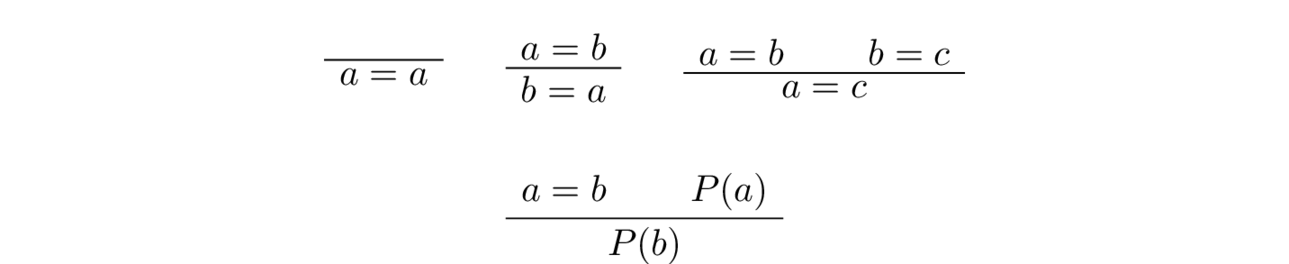
In Lean, the substitution rule is implemented by the term eq.subst. See the examples below. In the second example above (eq.symm e) is a proof of n = m constructed from the proof e of the proposition m = n using the symmetry of the equality predicate.
We say that a predicate $P$ discerns between objects $a$ and $b$ if exactly one of $P(a), P(b)$ holds, that is the following holds: \[ (P(a) \land \neg P(b)) \lor (\neg P(a) \land P(b)) \]
Here is an example of discernibility: Consider the parallel-line predicate and take a point $q$ on a line $\ell$, and consider the predicate $Q$ (ranging over lines) defined by \[ Q(m) = q \text{ lies on } m \] Now suppose $\pr{\ell}$ is a line parallel to $\ell$. Clearly, $Q(\ell)$ holds but not $Q(\pr{\ell})$. Therefore, the predicate $Q$ discerns between lines $\ell$ and $\pr{\ell}$.
Challenge (An Example of Discernibility in Real Numbers)
Find a predicate in the language of real numbers which discerns between $\sqrt{2}$ and $\sqrt{-2}$.
Challenge (An Example of Discernibility in Complex Numbers)
Can you find a predicate in the language of complex numbers which discerns between $i$ and $-i$?
Note that the converse of the substitution rule for equality does not hold: i.e. for some predicate $P$ it can well happen that $P(a) \iff P(b)$, but $a \neq b$: Consider the parallel-line predicate and fix a line $\ell_0$. Consider the predicate \[ P(m) = \text{line } m \text{ intersects with line } \ell_0 \] Now consider two parallel lines $\ell$ and $\pr{\ell}$ which are not identical. We have $P(\ell) \iff P(\pr{\ell})$ but $\ell \neq \pr{\ell}$.
Related to this discussion, there is an important philosophical principle which in some contexts equality is required to satisfy: This is the so-called identity of indiscernibles due to Leibniz is which states that there cannot be distinct objects or entities that have all their properties in common. That is, if for all predicates $P$, $P(a) \iff P(b)$ then $a=b$. This can be seen as the converse of substitution rule for equality. Consider the contrapositive of identity of indiscernibles: it states that if two elements are different then there is some predicate which distinguishes them (i.e. one of the elements has an attribute which the other does not possess.) This is known as the principle of dissimilarity of the diverse.
It is enlightening to find some predicates (other than equality of course) which fail the test of identity of indiscernibles, that is we are looking for two non-identical elements, say $a$ and $b$, located within some structure such that for no predicate $P$ discerns between them.
Equality in Lean
The notion of equality is more subtle than the treatment above might suggest: For instance you might have already seen the three equalities \[ 1 = 1.000\cdots \quad \text{ and } 0.\overline{9} = 0.999\cdots \quad \text{ and } 1 = 0.\overline{9} \] Note however, we already have few subtleties here: clearly the first two equalities are of not the same nature as the third one: In the second equality above we define $0.\overline{9}$ and in the first and third one we actually asserting two things, already defined, are the same. The first and third equalities are actually propositions which require proofs. One has to think a bit more carefully about equality, and fortunately for us there have been people, most notably the type-theorist Martin-Löf, who have contributed significantly to our understanding of equality.
In general, there are three different kinds of equality: That is for two well-defined terms $s$ and $t$ the expression $s=t$ can be either a
- syntactic equality, if $s$ and $t$ are made of the same syntax in the same way.
- definitional equality, if $s = t$ by virtue of a definition, e.g. $3 = 1 +1 +1$, and $n + 0 = n$ for a natural number $n$ in virtue of definition of sum of two natural numbers.
- propositional equality, if we can prove that $s=t$.
The last one is the “usual” kind of equality as understood by mathematicians, for instance “2+2 = 4”. An example of a definition equality which is not a syntactical one is $n + 0 = n $ (which holds by the definition of addition of natural numbers). Since definitional equality depends definition, it will also automatically depend on implementation details (that is, on exactly how things are defined under the hood). For instance we said $n + 0 = n$ is a definitional equality because $=$ is defined by recursion and the following clauses,
- $n + 0 = n$,
- $n + \suc(m) = \suc(m + n)$
We don’t want to get bogged down now with the details of the recursive definition above (what $\suc$ is, etc). The point is that $n + 0 = n$ because it is part of the package of the definition of $+$.
In Lean tactics such as exact and refl work up to definitional equality. For example, the following proof works:
example (n : ℕ) : n + 0 = n :=
begin
refl
end
However, the rewrite tactic rw won’t work because it works only for syntactic equality which n + 0 = n is not.