Propositions and Connectives
Table of contents
Introduction
In this lecture, we shall introduce propositional logic and we shall use it to analyze the forms of mathematical reasoning.
A map of Amsterdam is an an idealized model of Amsterdam. It depicts a caricature 2-dim image of buildings, Amstel river, various canals, roads, bicycle lanes, etc. We can consult a map to help us find the best route from one place to another. In a similar way, symbolic logic is an idealized model of mathematical reasoning. It is an idealization because the way we formalize proofs using sybmlogic logic is operationally different than how we conceive proofs in the first place: while formalized proofs are linear and mechanical, the way mathematicians come up with their proofs is non-linear and subjective. It is not at all unusual in mathematics that we believe something without possessing a complete proof and it also happens we might see a proof and still not believing it. While a good formal proof can tell us why a certian assertion holds, it may not neccessarily convince us that the assertion holds.
Although the psychological dynamics of symbolic proofs and proofs in practice are different, we can still use symbolic proofs as our guide or blueprint for finding our way in the jungle of proofs, or as an organizationl tool like a library, or as a recording tool similar to the way a paiting or a picture captures some aspects of reality. More importanly, with the help of computers and computer theorem provers, we can construct proofs whose validity can be checked only by computers.
Curiously, mathematicians did not formally study their proofs, as autonomous mathematical beings, until the 20th century. Once they did, they discovered a rich and beautiful calculus of proofs hidden under their feet. We are going to see some of its shiniest jewels in this course.
Although mathematicians’ interest in proofs is rather recent, philosophers, bishops, lawyers, and dedectives have been interested in proofs for much longer. Proofs arise anywhere one attempts to convince others. However, mathematical proofs are different in many respects than proofs found for instance in convincing a jury and the testing of medications. A mathematical proof, at least until now, have a certain nature to them: once we unserstand a mathematical proof then we are completely sure that it is valid. Ideally, proofs in mathematics are also not spatial or temporal: they do not depend when and where the proof is presented since the proof can be reconstructed in another place and time (but perhaps not its understanding).
Patterns of Reasoning
Our story begins around 350 BCE in Athens: that is about 2500 years ago. The protagonist is a middle-age Greek man named Aristotle. He was the first to study the patterns of reasoning in a formal fashion in his book ‘Prior Analytics’. The result of this work of Aristotle is known today as ‘syllogism’. The crucial insight of Aristotle was that the correctness of inferences of statements from other statements does not depend on the the content, truth or falsity of the individual statements, but, rather, the general patterns/rules of inference. We give two exmaples of this in below: The first one is from Prior Analytics and the second one too but with slight upgrade to include cyborgs.
- Example 1
- Every man is an animal. Every animal is mortal. Therefore every man is mortal.
- Every A is B. Every B is C. Therefore every A is C.
| Natural language | Symbolic | Aristotle’s symbolic notation | |
|---|---|---|---|
| assumption | Every man is an animal. | Every $A$ is $B$. | $BaA$ |
| assumption | Every animal is mortal. | Every $B$ is $C$. | $CaB$ |
| conclusion | Every man is mortal. | Every $A$ is $C$. | $CaA$ |
- Example 2
- Every human is mortal. No cyborg is mortal. Therefore no cyborg is a human.
- Every A is B. Every B is C. Therefore every A is C.
| Natural language | Symbolic | Aristotle’s symbolic notation | |
|---|---|---|---|
| assumption | Every human is mortal. | Every $N$ is $M$. | $MaN$ |
| assumption | No cyborg is mortal. | No $X$ is $M$. | $MeX$ |
| conclusion | No cyborg is a human. | No $X$ is $N$. | $NeX$ |
In the table above, from left to right, we abstract away from certain particularities to crystalise the logical form. This abstraction makes it possible to substitute various properties for $A$, $B$, and $C$. In below, we replicate the first table above, by substituting “being fish” for “$A$”, “being swimming creature” for “$B$”, and being “not horse” for “$C$”.
| Natural language | Symbolic | Aristotle’s symbolic notation | |
|---|---|---|---|
| assumption | Every fish is a swimming creature. | Every $A$ is $B$. | $BaA$ |
| assumption | Every swimming creature is not a horse. | Every $B$ is $C$. | $CaB$ |
| conclusion | Every fish is not a horse. | Every $A$ is $C$. | $CaA$ |
The various statements that result may come out true or false, but all the instantiations will have the following crucial feature: if the two hypotheses come out true, then the conclusion comes out true as well. We express this by saying that the inference is valid.
Logic is the study of the principles of valid inferences and demonstration. This conception of logic indicates that its application might go beyond mathematics itslef, and indeed this is the case: In computer science, logical tools and methods play an essential role in the specification, and verification of computer hardware and software.
A typical inference has few hypotheses (or none at all) and a conclusion. In the example above, and in fact all of the examples cited by Aristotle, there are only two hypotheses. We sometimes call a hypothesis an assumption. If we denote the proposition “Every $A$ is $B$” by $P$ and the proposition “Every $B$ is $C$” by $Q$ and the proposition “Every $A$ is $C$” by $R$, then from the hypotheses $P$ and $Q$ we derived $R$. This we display with a proof tree:
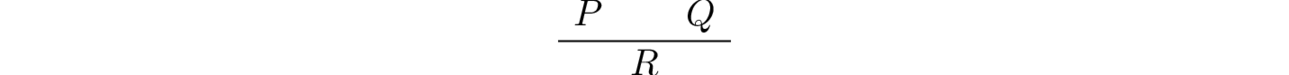
The line seperates assumptions from conclusions: All that is written above the line are the assumptions and all that is written below the line is the conclusion.
In mathematics texts we often see expressions like “so”, “consequently”, “hence”, and “therefore” are used to indicate that a claim that is being made is is the conclusion of an argument. In our proof tree above we could say:
Since $P$ and $Q$ are the case, therefore $R$ is the case.
or,
$R$ follows from $P$ and $Q$.
or,
$P$ and $Q$ entail $R$.
Propositions
The definition of what a proposition should be has been a contentious issue in philosophy and the philosophy of language for a long time:
- Aristotle held that a proposition is a sentence which affirms or denies a predicate of a subject.
- Wittgenstein held that a proposition is the set of possible worlds/states of affairs in which it is true.
- Others thought propositions are declarative sentences which are truth-bearers, i.e. they are either true or false.
- Frege held that propositions are not physical entities.
- Some philosophers of mind believe that propositions are mental entities.
There are serious issues with all these views: how does the proposition “it is raining now” fit with the first view, how does the second view distinguishes between the proposition “1+1=2” and “2+2=4”, how does third view account for the propositionality of the statement of Riemann Hypothesis (or any other open problem of mathematics), etc.
For us propositions are assertions that can be judged to be true or false. This view comes quite close to what Aristotle conceived proposition to be: a proposition is a particular kind of sentence (a declarative sentence) that affirms or denies a predicate of a subject. Examples are “All men are mortal” and “Socrates is a man.” More mathematical examples are , “.99999… = 1”, and “678123 is a composite number”.
Atomic propositions are assertions that can be judged to be true or false without depending on other propositions truth values. Examples of atomic propositions are: “5 is a prime”, “5+7 = 12” and “program $P$ terminates”. In contrast the proposition “if program $P$ terminates it will output 1.94873” is not atomic. Other Propositional formulae are constructed from atomic propositions by using logical connectives.
Following the Swedish philosopher and logician Martin-Lof we take the meaning of a proposition to be determined by what counts as a verification/witness/proof of it. Therefore, the meaning of proposition “1+1=2” is given by proofs of “1+1=2”. In this interpretation, we say a proposition is true (or is the case, or holds) precisely when we have a proof of it. A proposition $P$ is false if there is a proof which demonstrates the impossibility of $P$ being true.
In Lean we declare that $P$ is a proposition by writing
P : Prop
Try `prop` instead of `Prop` in above: what error do you get?
some message
We postulate (aka hypothesize) that any proposition $P$ is true by introducing a variable hp of type P as follows:
variable hp : P
Note that the naming of the variable hp does not matter, we could have as well written p : P or my_assumption : P, or even any_word_you_like : P.)
In short, h : P means that h is a proof of P, or you can regard h as an assumption that P is true; logically these are the same. When we compile our code in Lean, in the viewer window (in VSCode or the Lean web editor) we see the ⊢ symbol. This symbol is called “turnstile” in logic. It means whatever is to the left of it are the assumptions and the stuff to the right of it are the goals we are trying to prove. Note that the goals Lean change dynamically as we progress line-by-line through our proof.
Tautologies
A proposition is called a tautology if it can be derived from no assumption at all. For instance the proposition “if $1=2$ then $1=2$” is a tautology while the proposition “$1+1=2$” is not.
Equivalence of Propositions
Two propositions $P$ and $Q$ are equivalent if assuming $P$, we can derive $Q$ and vice versa (that is, if assuming $Q$, we can also derive $P$).
New Propositions From Old
Using simple (aka atomic) propositions such as “The sun is shining” and “It is raining” we can form the more complicated proposition “The sun is shining and It is raining”.
That required us to first unquote the sentences, insert an “and” and then put a quote around the resulting sentence.
In this way, we can make new propositions from old propositions using connectives (such as “and”). For each connective, we specify a rule to introduce a proof of the compound proposition using that connective (the so-called introduction rule) and a rule to use or eliminate such a proof.
We call a compound proposition (such as “The sun is shining and It is raining”) a propositional formula. We also introduce a formal deductive system to prove propositional formulas. There are a number of such systems: linear ND system, sequent calculus, Fitch system, Hilbert system, etc); the one we will use is called natural deduction, designed by Gerhard Gentzen in the 1930s. In natural deduction, every proof is a proof from hypotheses. In other words, in any proof, there is a finite (possibly empty) set of hypotheses $P_0, P_1, \ldots, P_n$ and a conclusion $Q$, and what the proof shows is that $Q$ follows from $P_0, P_1, \ldots, P_n$.
Conjunction
The conjunction of propositions $P$ and $Q$ is denoted by $P \land Q$ and is read as “$P$ and $Q$”. In Lean we write P ∧ Q (you can type the symbol by typing \and an pressing tab or space keys on your ⌨️.)
varibales P Q : Prop
#check P ∧ Q
But what is $P \land Q$ now other than a meaningless symbol? It is not just enough to say that $\land$ means “and”; we have to also say how is the truth of $P \land Q$ is related to the truth of $P$ and the truth of $Q$. The meaning of $P \land Q$ is given by the following rules.
- Conjunction Introduction: If $P$ is true and $Q$ is true, then $P \land Q$ is true. That is, to supply a proof of $P \land Q$ we need to supply a proof of $P$ and and a proof of $Q$.
- Conjunction Elimination: Conversely, if $P \land Q$ is true, then $P$ is true and $Q$ is true. That is, a proof of $P \land Q$ yields a proof of $P$ and a proof of $Q$.
In natural deduction the conjunction introduction rule is displayed by the following inference rule: 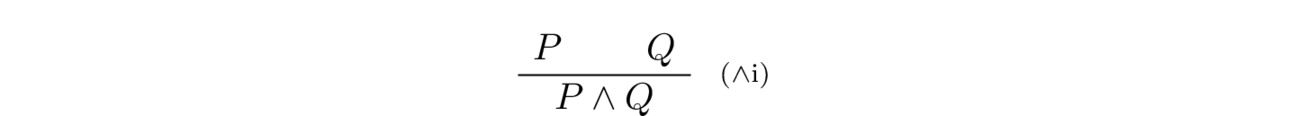
The embellishment $\mathord{\wedge}\mathrm{i}$ on the right side of the inference line indicates that this rule is an introduction rule for the conjunction connective. The conjunction elimination rule is displayed by the following inference rule:
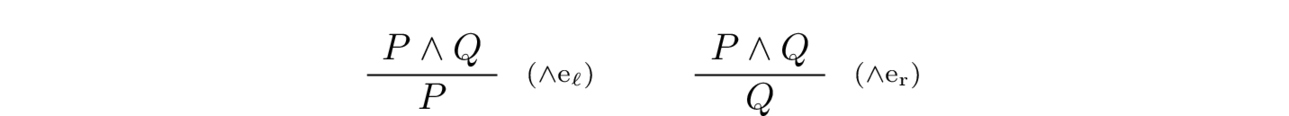
The introduction and elimination rules of conjunctions are baked into Lean; Let’s check the type of expression and.intro hp hq.
variables P Q : Prop
variable hp : P
variable hq : Q
#check and.intro hp hq
The command #check is outputting the type of well-formed expressions written in front of it. For instance when we write in Lean
#check 2
we get 2 : ℕ. Beware however #check and.intro hp hq is not a proof of P ∧ Q. The following Lean code corresponds on the nose to the $\land$ introduction rule:
variables P Q : Prop
example (hp : P) (hq : Q) : P ∧ Q := and.intro hp hq
The conjunction elimination rule is written in Lean as follows:
variable h : P ∧ Q
#check and.left h
#check and.right h
Here and.left h and and.right h are respectively proofs of P and Q constructed from the proof h of P ∧ Q. The expression and.left corresponds to $\mathord{\wedge}\mathrm{e_\ell}$ and and.right corresponds to $\mathord{\wedge}\mathrm{e_r}$.
Note that if you put the code snippet above into Lean it will complain unknown identifier 'P' since we really have not introduced variables P and Q, and Lean has no way of guessing what the type of P and Q are.
But once we introduce P and Q then things work out.
variables P Q : Prop
#check P ∧ Q
variable h : P ∧ Q
#check and.left h
#check and.right h
From the simple introduction and elimination rule of conjunction alone, we can derive few conclusions. For instance, that the conjunction connective is commutative, i.e. a proof of $P \land Q$ yields a proof of $Q \land P$ and vice versa. This means that the order of conjoining two propositions does not matter.
Here is a natural deduction proof of the commutativity of conjunction.
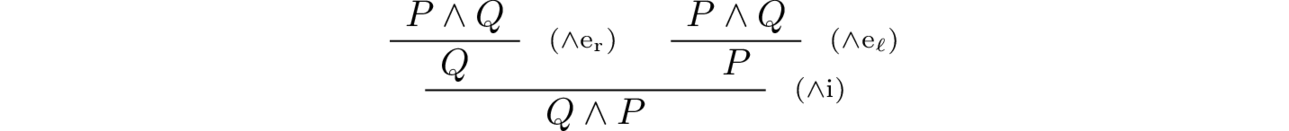
And the Lean proof term is given by the expression and.intro (and.right h) (and.left h):
variable h : P ∧ Q
#check and.intro (and.right h) (and.left h)
✏️ Challenge
In below we have constructed a proof term in Lean:
variable P : Prop
variable h : P ∧ P
#check and.left h
that the conjunction connective is idempotent, that is for every proposition $P$, the proposition $P \land P$ is equivalent to $P$.
Can you construct the corresponding natural deduction proof tree?
Implication
Here are few examples of implication connective in forming various sentences; It often appears in the form of “if … then …”.
- Alice is tall. Therefore if Alice is strong, then Alice is both strong and tall.
- If $T$ is a triangle, then it is most likely not an equilateral triangle.
- A neuron fires an action potential if its membrane potential reaches the threshold of $-55$ mV.
- If $4 * 5 = 19$ then $m = n$ for all natural numbers $m$ and $n$.
- If $p$ is a prime number, then if $p$ is even, then $p=2$.
- If $p$ is a prime number, then $p$ is even if and only if $p=2$.
The implication $P \Rightarrow Q$ is a new proposition built from $P$ and $Q$ and we read it as “if $P$ then $Q$”. The implication is a form of hypothetical reasoning. On the supposition that $P$ holds, we argue that $Q$ holds as well. If we are successful, we have shown that $P \To Q$, without supposing $P$. The implication is used in all sorts of scientific hypothesis-making (e.g. the second example above). We can also think of implication as a habit, cause, or promise (eg. I become thirsty if I run, or I burn my fingers if I touch boiling kettle, etc).
Our main interpretation of an implication $P \To Q$ is a procedure which transforms proofs of $P$ into proofs of $Q$.
The following are the inference rules of implication:
- Implication Introduction: If from the assumption that $P$ is true we can derive that $Q$ is true, then $P \Rightarrow Q$ is true. Note that we actually do not know whether $P$ is true; all we know is that in the presence of $P$, the proposition $Q$ is true.
- Implication Elimination: If we have a proof of $P \Rightarrow Q$, that is a hypothetical proof of $Q$ from $P$, and we have a proof of $P$, then we get a proof of $Q$. This is known as modus ponens1.
In contrast to conjunctive connective, the implication has only one elimination rule. The natural deduction presentation of introduction and elimination rules is at once shown in below:
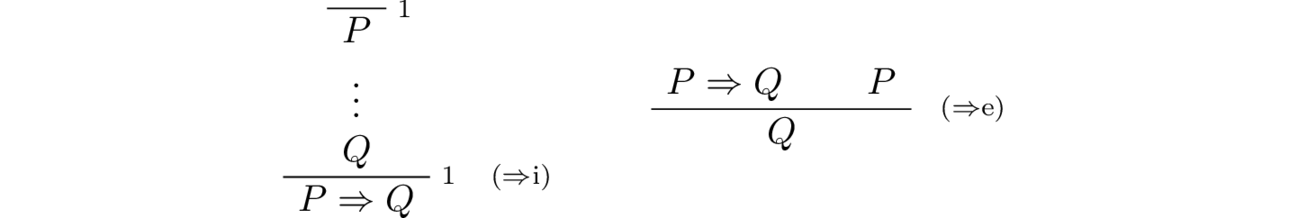
The implication introduction rule is a tricky one, because it can cancel a hypothesis: In the last step, to derive $P \Rightarrow Q$, we cancel the assumption that $P$ is true which was marked by “$1$” (used to indicate that this was our first – and only – assumption). Since we derived $P \Rightarrow Q$ after cancelling the assumption “1” out, it means that we have proved the proposition $P \To Q$ under no assumption and only by our construction of a proof of $Q$ from any proof of $P$. In more detail, if we can infer a proposition $Q$ from a proposition $P$ then you have “$Q$ is true” under the assumption “$P$ is true”. Note that $Q$ may not be true on its own since we need to assume $P$.
In Lean, we denote an implication by $\to$ instead of $\Rightarrow$ (This is achieved by typing \to into your VSCode editor).
Again, Lean knows about introduction and elimination rules of implications: Suppose p is the premise that P is the case and q is proof of Q, possibly involving p. Then a proof of P → Q is given by the expression assume p : P, q. For example, we can construct a proof of A ∧ B → B ∧ A as follows:
variables A B : Prop
#check (assume p : A ∧ B, and.intro (and.right p) (and.left p))
✏️ Challenge
Can you present the proof above in a proof tree?
For every proposition $P$ the proposition $P \Rightarrow P$ is a tautology:
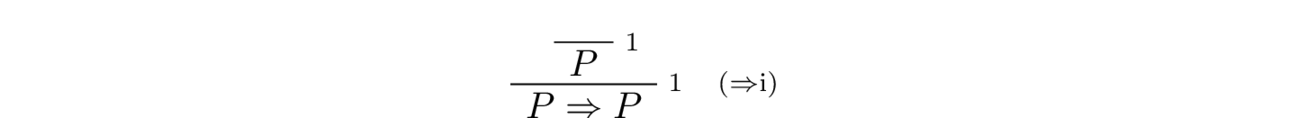
We now try to construct a Lean proof of the theorem $P \Rightarrow P$. First let us consider the following term.
variable P : Prop
#check (assume hp : P, hp)
There is another way of writing the same proof which uses very simple tactics intro and exact. We will learn more about tactics as we progress.
let us think of tactics using the following simile: An informal mathematical proof might go as follows: “To prove the forward direction, first unfold the definition,then apply the previous lemma, and specialize the result to when $x$ is a blah.” These are instructions given by the author to the reader for finding find the relevant proof that the author has in mind. In a similar way, tactics are instructions that we tell proof assistants (in our case Lean) to construct a proof term. Like informal proofs, proof tactics support an incremental style of writing proofs, in which you unfold a proof and work on goals one step at a time.
In this lesson we are going to learn about the following tactics, but as the course progresses, so does the number of tactics we use.
introexactapply
Our first tactic, namely the tactic intro in below, is used to add a new hypothesis hp (which hypothesizes that that the proposition P is true) to the local context of the proof. More generally, if the goal is to prove P → Q, then intro hp puts hp : P in the local context and the new goal target is Q. The intro tactic corresponds to the Introduction rule of
Our second tactic exact is perhaps the simplest tactic: If we have an assumption hp that P is true, and we want to prove that P is true, then exact hp will solve this goal.
In Lean, if our goal is ⊢ P and we have a hypothesis hp : P then exact h will solve it, i.e. we will have no more goals to achieve. The following Lean proof, of the proposition that a proposition $P$ implies itself, uses precisely the tactics intro and exact.
variable P : Prop
example : P → P :=
begin
intro hp,
exact hp,
end
⚠️ Note
In the tactic mode, we must use a , after each tactic for Lean to know that we are done. If we write the code above, but omitting ,, say the first one, Lean gives the error
unknown identifier 'exact'
since Lean thinks exact is an argument for intro tactic since we did not close the intro hp with a ,.
Finally, the tactic apply corresponds to the elimination rule of implication. In mathematics, it can be used to show a certain corollary of a theorem (theorems are often in the form of an implication). For instance, consider the following theorem first proved by Euler2:
Theorem If $a$ and $n$ are coprime positive integers then $n$ divides $a^{\varphi(n)} -1$, where $\varphi (n)$ is Euler’s totient function.
We obtain another theorem (the so called Fermat’s little theorem ) by choosing $n$ to be a prime number in Euler’s theorem.
Theorem If $a$ is an positive integer and $p$ is a prime number then $p$ divides $a^p - a$.
Still if we choose $a = 2$ in the previous theorem, we obtain the following corollary:
Corollary If $p$ is a prime number then $p$ divides $2^p - 2$.
Now, our corollary has the form of an implication and whose proof is constructed from the proof of more general Euler’s theorem. If we have a proof that $p$ is prime then we obtain a proof that $p$ divides $2^p - 2$. We know that $43223$ is a prime number (supposing that we have verified that $1$ is the only number below it which divides it.) Therefore we can apply the corollary above to $43223$ and therefore, we conclude that $43223$ divides $2^{43223} -2$.
More formally, if we’re trying to prove a proposition Q, and we have a proof h : P → Q, then it suffices to prove P. So apply h, changes the goal from Q to P. The key point here is that apply h will only work when h is an implication, and it will only work when the conclusion of h matches the goal. Here is an example:
example : ((P → Q) ∧ P) → Q :=
begin
intro h,
apply and.left h,
exact and.right h,
end
Notice the change of goals, from Q to P, in the third and fourth lines above.
✏️ 🤖 Challenge
This Challenge is a bit harder and it uses all the tactics we have learned so far, namely intro, exact, and apply. 🤖 has started to prove it but 🤖 was stock and got bored and has left us a “sorry” note. Can you help 🤖 achieve its goal by filling in sorry?
example: (((P → Q) → Q) → Q) → P → Q :=
begin
intro hpq,
intro hp,
apply hpq,
intro u,
sorry,
end
Sometimes instead of the combination of apply followed by an exact tactic – as in the last two examples – we prefer to have a one-liner application of a proof h of P → Q to a proof p of P: This is achieved by the expression h p that is h followed by p. If h and p are compound expressions, we put parentheses around them to make it clear where each one begins and ends. In Lean the formations of implications associates to the right and the applications associate to the left: This means the expression P → Q → R is interpretted as P → (Q → R) and the expression h1 h2 h3 is interpreted as (h1 h2) h3.
Example
If we have a proof $q$ of $Q$ we can derive $P \Rightarrow Q$ for any proposition $P$ whatsoever, without even needing a proof $P$. That is The natural deduction proof true:
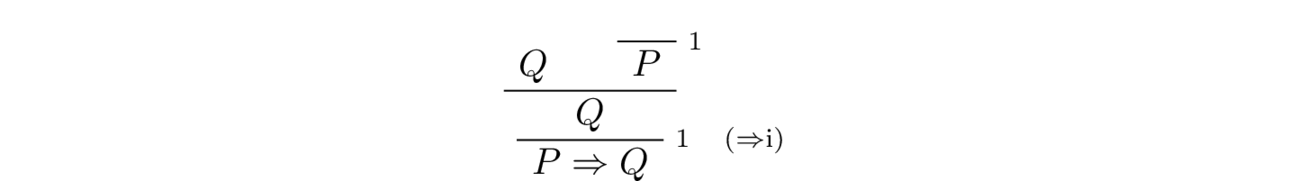
How many cancellations did we perform?
We can even prove that $Q \Rightarrow P \Rightarrow Q$ is a tautology for all propositions $P,Q$. Here is a Lean proof involving tactics intro and exact.
variables P Q : Prop
example : Q → P → Q :=
begin
intro hq,
intro hp,
exact hq,
end
✏️ Challenge
Can you present the (natural deduction) proof tree associated to the Lean proof above?
Example
Let’s give an example of usefulness of the natural deduction proof trees in capturing the logical core of some kind of arguments we use every day in our lives.
Alice is tall. Therefore if Alice is strong, then Alice is both strong and tall.
The first task is to identify the atomic propositions in the argument above. Let’s denote the proposition “Alice is strong” by $S$, and the proposition “Alice is tall” by $T$.
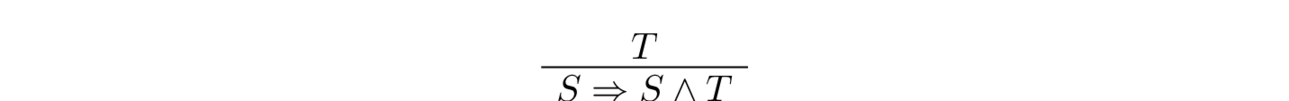
✏️ Challenge
Can you translate the argument above to Lean?
variables P Q R: Prop
variable f : P → Q → R
variable p : P
variable q : Q
#check (assume h : P ∧ Q, f (and.left h) (and.right h))
We will give another example of the interaction between the connectives $\Rightarrow$ and $\land$: we will prove that for propositions $P,Q,R$ the compound proposition $(P \Rightarrow Q) \land (Q \Rightarrow R) \Rightarrow (P \Rightarrow R )$ is a tautology. First note the connectives $\land$ and $\lor$ bind faster, and therefore, this proposition formula above has a unique reading: it is the same as $\big( (P \Rightarrow Q) \land (Q \Rightarrow R)\big) \Rightarrow (P \Rightarrow R )$. Let’s write $A$ for $P \Rightarrow Q$ and $B$ for $Q \Rightarrow R$ and $C$ for $P \Rightarrow R$. We want to prove the proposition $A \land B \Rightarrow C$. We know only one way to prove an implication, and that is by the implicaiton introduction rule. So, we have to show that under the assumption $A \land B$, the proposition $C$ holds. But now $C$ itself is the implication $P \Rightarrow R$ and to prove it we assume $P$. Hence altogether our assumptions are $A \land B$ and $P$. We can use the conjunction elimination derive $A$ and $B$, i.e. $P \Rightarrow Q$ and $Q \Rightarrow R$. Now, by implication elimination, from $P$ and $P \Rightarrow Q$ we derive $Q$ which combined with $Q \Rightarrow R$ entail $R$. We can draw the full natural deduction proof tree which encapsulates this argument into a tree:
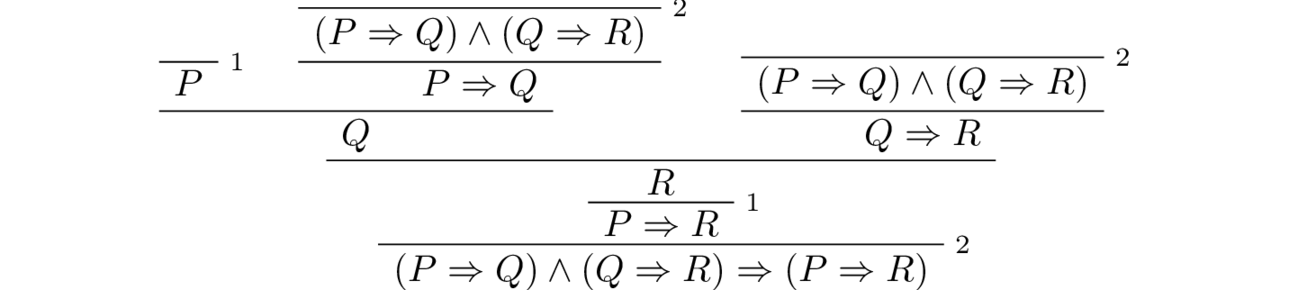
✏️ Challenge
Try to complete a Lean proof of $(P \Rightarrow Q) \land (Q \Rightarrow R) \Rightarrow (P \Rightarrow R )$ by replacing sorry in the code below with a single-line expression.
variables P Q R : Prop
example : (P → Q) ∧ (Q → R) → (P → R) :=
assume hpqr : (P → Q) ∧ (Q → R),
assume p : P,
sorry
Warning
A commonly found mistakes students make is in denoting a chain of implications: If we have some propositions $P_1, \ldots, P_n$ and we want to say that $P_1$ implies $P_2$, $P_2$ implies $P_3$ and so on, i.e. for every $i \leq n-1$, $P_{i-1}$ implies $P_i$.
This means that we know all the propositions $(P_1 \To P_2) \, , \, (P_2 \To P_3) \, , \, \ldots \, , \, (P_{n-1} \To P_n)$ to be true. We can conclude that $P_1 \To P_n$ is true essentially by the same proof as above. Therefore, $(P_1 \To P_2) \land (P_2 \To P_3) \land \ldots \land (P_{n-1} \To P_n) \To (P_1 \To P_n)$.
However, what we should avoid writing is $P_1 \To P_2 \To \ldots \To P_n$ since this proposition is entirely different than our assumptions and conclusions.
✏️ Challenge
- Show that under the assumption that $P_1 \To P_2$ is true we can derive $P_1 \To P_3$ from $P_1 \To P_2 \To P_3$.
- Fill in the
Leanproof of part 1:variables P_1 P_2 P_3 : Prop example : (P_1 → P_2) → (P_1 → P_2 → P_3) → (P_1 → P_3) := assume h, assume k,
Disjunction
The disjunction of $P$ and $Q$ is denoted by $P \lor Q$ and is read as “$P$ or $Q$”. The rules of inference concerning disjunction are as follows:
- Disjunction Introduction: $P \lor Q$ is true whenever either $P$ is true or $Q$ is true. That is to verify the truth of $P \lor Q$ we need to either verify $P$ or verify $Q$.
- Disjunction Elimination: To prove a proposition $R$ from $P \lor Q$ we have to do two things: prove $R$ under the assumption $P$ and prove $R$ under the assumption $Q$. In other words, if we know that $P \lor Q$ is true, we must consider two cases: $P$ true and $Q$ true. If we can prove a conclusion $R$ true in both cases, then $R$ must be true!
The natural deduction presentation of introduction rules for disjunction is shown in below:
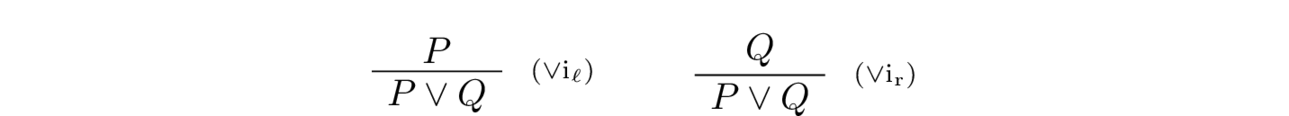
As you might have noticed, the elimination rule for disjunction is more complicated than the introduction rules, and this is also reflected in the natural deduction presentation of
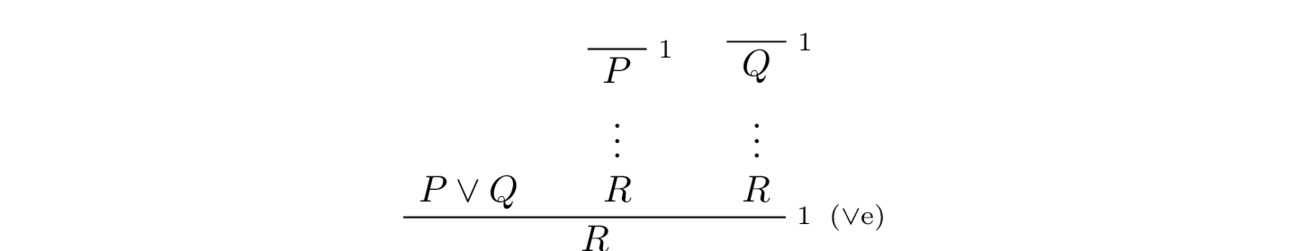
Note that in the proof tree above, the assumptions $P$ and $Q$ get cancelled out in the last line of deduction, but the assumption $P \lor Q$ remains uncancelled (this makes since since otherwise, we could prove any proposition $R$ from thin air!)
✏️ Challenge
Give two proofs of the tautology \(P \land Q \To P \lor Q \). Think about whether this two proofs are the same.
The expressions or.inl and or.inr in Lean correspond to the introduction rule of disjunction: For instance, if we have a proof hp of a proposition P, by the introduction rule, for any propositon Q we get a proof or.inl(hp) of proposition P ∨ Q, and for any propositon R a proof or.inr(hp) of proposition R ∨ P.
✏️ 🤖 Challenge
Below is a Lean proof of the previous tautology. How do you write your other proof in Lean?
example : P ∧ Q → P ∨ Q :=
begin
intro h,
exact or.inl (and.left h)
end
✏️ 🤖 Challenge
In below, 🤖 has started to prove in Lean that the proposition
\[ (P \To R) \land (Q \To R) \To (P \lor Q ) \To R \]
is a tautology. But, 🤖 was stock and got bored and has left us some “sorry” note. Can you help 🤖 achieve its goal by filling in “sorries”?
example : (P → R) → (Q → R) → (P ∨ Q → R) :=
begin
intro hpr,
intro hqr,
intro hpqr,
cases hpqr,
{
sorry,
},
{
sorry,
},
end
Falsity
Sometimes we need to work with propositions which are always false such as “A bachelor is married”, or $0=1$. When we develop mathematical theories, we postulate certain axioms and try to prove interesting theorems (other statements) from these axioms. An early example is Euclid’s postulates of plane geometry in terms of points, lines, angles, and circles.
- A straight line segment can be drawn joining any two points.
- Any straight line segment can be extended indefinitely in a straight line.
- Given any straight lines segment, a circle can be drawn having the segment as radius and one endpoint as center.
- All right angles are congruent.
- If two lines are drawn which intersect a third in such a way that the sum of the inner angles on one side is less than two Right Angles, then the two lines inevitably must intersect each other on that side if extended far enough.
From Axiom 5, it follows that
- Through any given point can be drawn exactly one straight-line parallel to a given line.
In fact this statement is equivalent to the fifth postulate (for this reason, sometimes called the Parallel Postulate).
The purpose of Euclid axiomatization of geometry was that if one starts from some basic postulates which include notions (such points and lines), constructions (a line connecting any two points), and axioms (all right angles are equal), once deduces consequences logically. For instance the statement “6” above is such a consequence.3
It is crucial that when we build mathematical theories (such a the theory of Euclidean geometry), we have to make sure that no false statements will be a consequence of our postulates. For instance, in a theory of numbers, we should not be able to derive $0=1$. But, to prove the impossibility of deriving false statements, we need to have a way to talk about falsity.
We introduce the symbol $\bot$ for a general false statement (aka absurdity).
Fasle Introduction: $\bot$ has no introduction rule; we do not want to have a way to produce falsity.
Fasle Elimination: $\bot$ has one introduction rule known as the principle of explosion (aka ). It states that that if $\bot$ is derived, then any proposition follows. This implies that if $\bot$ is true then everything is true and therefore, truth becomes degenerate: everything is false and true at the same time.
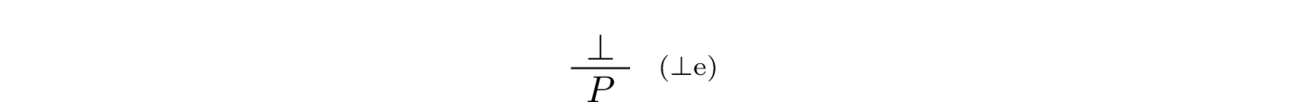
In Latin the name of this principle ex falso quodlibet (“from falsehood, anything”). The word quod roughly means whatever and libet roughly mean pleases. Variants of the principle’s name include ex falso sequitur quodlibet, “from falsehood, anything follows”, and ex contradictione (sequitur) quodlibet, “from contradiction, anything (follows)”.
✏️ Challenge
Show that for any proposition $P$, the proposition $\bot \To P$ is a tautology. In particular, we have a proof of $\bot \To \bot$
Negation
The negation of a proposition $P$, denoted by $\neg P$, is the proposition whose proofs are the refutations of $P$. Therefore, a proof of $\neg P$ should demonstrate the impossibility of any proofs of $P$. This justifies the following rules:
- The negation of $P$ is denoted by $\neg P$ and is read as “not $P$”.
- Negation Introduction: $\neg P$ is true when an absurdity (such as $0=1$) can be derived from the assumption that $P$ is true. Since all absurdities are equivalent, we denote a generic one of them by $\bot$.
- Negation Elimination: If $\neg P$ and $P$ are both true, then we get an absurdity (aka get a contradiction). This means it cannot be the case that contradictory premises $P$ and $\neg P$ hold.
Note that combining the elimination rule of $\neg$, and the elimination rule of $\bot$, we infer that from contradictory premises anything follows (ex contradictione quodlibet).
✏️ Challenge
Prove that for any proposition $P$, the propositions $\neg P$ and $P \To \false$ are logically equivalent.
In fact, in Lean this is the way how the negation is defined.
(Latin for “method of putting by placing”). ↩
Euler provided the first published proof in 1736, in a paper titled “Theorematum Quorundam ad Numeros Primos Spectantium Demonstratio” in the Proceedings of the St. Petersburg Academy,[6] but Leibniz had given virtually the same proof in an unpublished manuscript from sometime before 1683 ↩
This is in contrast with analytic geometry, where notions such as points and lines are represented concretely using cartesian coordinates in $\R^n$—lines are sets of points—and the basic constructions and axioms are derived from this representation. ↩