Excluded Middle

Table of contents

1. Law of Excluded Middle and Constructive Mathematics
2. Proof by Contradiction

Law of Excluded Middle and Constructive Mathematics

… Nature does nothing by leaps and bounds; she prefers gradual transitions and on a large scale too keeps the world in a transitional state between imbecility and sanity. But jurisprudence takes no notice of this. It says: non datur tertium sive medium inter duo contradictoria; in plain English: the individual is either capable of acting to law or he is not, for between to contraries there is no third or middle term. As a result of this capacity he becomes liable to punishment; as a result of his quality of being liable to punishment he becomes legally a ‘person’, and as a ‘person’ in the legal sense he has a share in the suprapersonal benefits of the law. Concerning Moosbrugger, Excursion into the realm of logic and moral, The Man Without Qualities, Robert Musil

Taking the principle of excluded middle from the mathematician would be the same, say, as proscribing the telescope to the astronomer or to the boxer the use of his fists. To prohibit existence statements and the principle of excluded middle is tantamount to relinquishing the science of mathematics altogether.¹

It is fairly difficult to explain to a classical mathematician the reasons for rejecting LEM, because constructive and classical mathematicians use the same words to mean different things. The result is that to classical mathematicians the constructive ones are like ascetic monks who took some LSD, while to constructive mathematicians the classical ones are like beings from a two-dimensional world who cannot grasp a third dimension. So take some LSD and imagine yourself sitting inside a sheet of paper.²

Most mathematicians are not well-versed in logic by training: In fact, most of them have the view that logic, may be interesting on its own, has no or little bearing for the rest of mathematics. In certain respects, this looks plausible, but a deeper understanding of logic and foundations adds complications to this simple narrative. At any rate, since this view is commonplace in the mathematical community, most mathematicians do not bother to learn about varieties of logic(s). This might explain why it is so common for mathematicians to take the Law of Excluded Middle (LEM) for granted. Interestingly, this law, says that

For every proposition $P$, either $P$ or $\neg P$ holds.

In other words,

For every proposition $P$, either $P \lor \neg P$ is a tautology.

To many this is a self-evident truth. For instance, Aristotle assumed it to be self-evident, although he did not explicitly give a name to this principle. In Latin, the law of Excluded Middle is called tertium non datur (“no third possibility is given”), and sometimes, principium tertii exclusi (“the principle of excluded third”). We shall use the abbreviation LEM for the Law of Excluded Middle.

We should remark that many neat (classical) proofs depend on LEM. Just to give one of many such neat proofs, we investigate the following proof of the so-called Fundamental Theorem of Arithmetic. This theorem states that every integer greater than 1 either is prime or factors as the product of primes numbers, and moreover, that this factorisation is unique up to reordering of factors. Therefore, this theorem has two parts, first one has to establish the existence of factorization of every number into products of prime numbers, and secondly, the uniqueness, i.e. any two such factorizations are the same.

Consider the following proof from Edmund Landau’s number theory book (“Vorlesungen über Zahlentheorie Aus der elementaren Zahlentheorie”, 1927) which proves the existence part of the Fundamental Theorem of Arithmetic:

Did you spot the application of Excluded Middle? Landau uses LEM in his proof exactly where he writes:

Ist $a$ Primzahl, so ist die Behauptung richtig. Anderfalls … (If $a$ is a prime integer then we are done, otherwise … )

Prima facie, in his deduction Landau uses $P \lor \neg P$, where $P$ is the proposition “$a$ is prime”, as a tautology and then argues by cases: if $P$ is the cases some other proposition $R$ follows, and if $\neg P$ is the case again $R$ follows. Finally he uses disjunction elimination to conclude the desired $R$ follows (although, this last part is usually left implicit in informal proofs.)

However, note that this is an avoidable use of Excluded Middle: That is we can construct a proof of $P \lor \neg P$, where $P$ is the proposition “$a$ is prime”, without using the LEM: Whether a number is prime or not, is decidable meaning there is an (effective) algorithm which upon getting any natural number as input, determines whether that number is prime or not. A simple primality-test program (in Python) based on the idea of Sieve of Eratosthenes is given in below:

def is_prime(n: int) -> bool:
    if n <= 3:
        return n > 1
    if n % 2 == 0 or n % 3 == 0:
        return False
    i = 5
    while i ** 2 <= n:
        if n % i == 0 or n % (i + 2) == 0:
            return False
        i += 6
    return True

Since Intuitionist and constructive mathematicians reject LEM. The Dutch mathematician L.E.J. Brouwer proposed that the law of excluded middle should not be regarded as an admissible logical principle, and he had serious doubts concerning the truth of this law. In Brouwer’s view, the law of excluded middle is an instance of a hasty and ultimately wrong generalization of logic of finite mathematics to the logic of infinite mathematics.³

But note that this does not mean intuitionists admit the negation of LEM as a logical principle! The sense in which LEM is rejected is more subtle and we will know more about it as we progress. Note that no matter how hard we try, we fail to construct, for every proposition $P$, a proof of $P \lor \neg P$ using the intuitionistic rules of inference we have learnt. In fact, it can be proven that $P \lor \neg P$ cannot be proven in the intuitionistic logic, but for this we need more advanced tools such as the Kripke semantics (aka many-world semantics) of propositional logic, and the fact that it is a complete semantics, which is beyond the scope of this short lesson.

Classical mathematicians, i.e. those who believe in the LEM, take LEM as an axiom in their system, that is they believe it (since they think it is a self-evident truth) without actually giving a proof of it.

Alonzo Church, the inventor of Lambda Calculus – the first programming language – in his article On The Law Of Excluded Middle wrote

Taking this [Brouwer’s] point of view, we may accept a system of logic in which the law of excluded middle is assumed, a system in which the law of excluded middle is omitted without making a contrary assumption, and a system which contains assumptions not in accord with the law of excluded middle as all three equally admissible, unless one of them can be shown to lead to a contradiction. If we had to choose among these systems of logic, we could choose the one most serviceable for our purpose, and we might conceivably make different choices for different purposes.

Challenge

Show that LEM does not imply that there is a proposition which is neither true nor false!

Proof by Contradiction

A law of classical logic closely related to Law of Excluded Middle (LEM) is the Law of Double Negation (LDN) .This law states that

For every proposition $P$, the propositional formula $\neg \neg P \To P$ is a tautology.

Note that using the intuitionistic rules of inference we can prove, for every proposition $P$, that the formula $P \To \neg \neg P$ is a tautology:

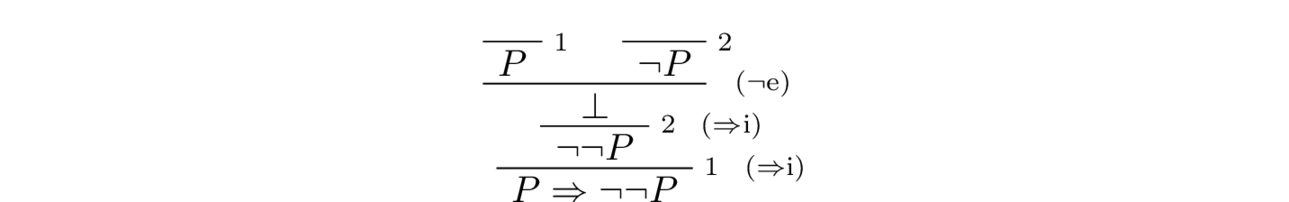
The Law of Double Negation postulates validity of the converse of this implication. Note that in the presence of LDN, we have the following inference

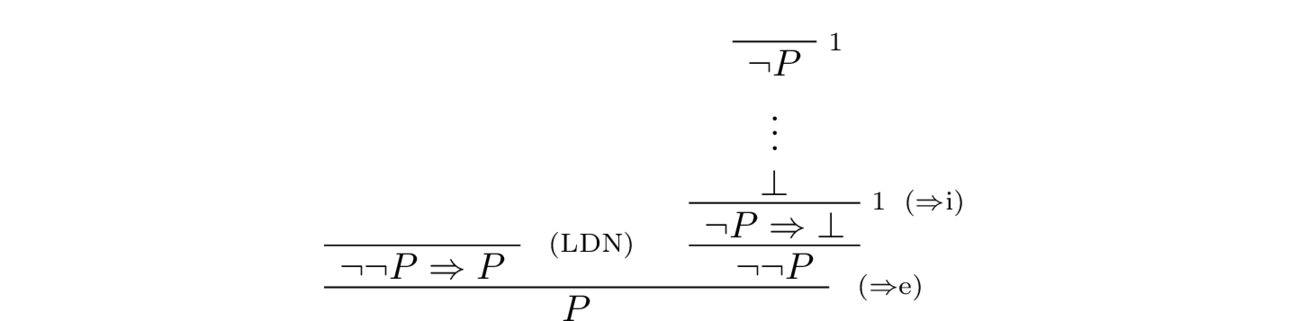
That is if from $\neg P$ we derive $\bot$, then we can conclude that $P$ holds; In other words, in the presence of LDN, a proof of impossibility of $\neg P$ is a proof of $P$. Therefore, if we assume LDN, we have the following proof strategy:

For every proposition $P$, if $\neg P$ fails to hold, then $P$ holds.

A proof of $P$ from a proof of impossibility of $\neg P$ is what often called a proof by contradiction (or reductio ad absurdum). Therefore, a proof by contradiction is an inference rule which says

To prove $P$, assume $\neg P$ and derive absurdity.

In natural deduction, proof by contradiction is expressed by the following pattern:

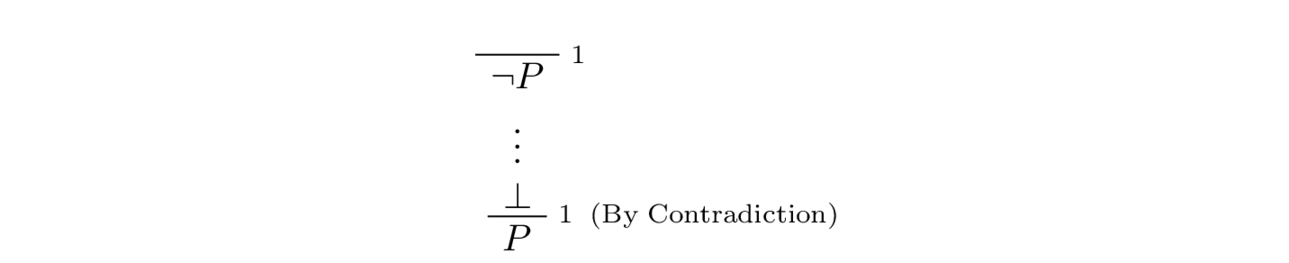
We take note that the assumption $\neg P$ is canceled at the final inference.

Proof by Contradiction vs Proof of Negation

There is a subtle point to be made to distinguish two kinds of proofs: If a statement that we want to prove is negative, i.e. it is of the form $\neg P$ for some other proposition $P$, then by the negation introduction rule, to prove $\neg P$ we assume $P$ and derive absurdity $\bot$. However, if the proposition $P$ to be proved is positive (i.e. it does not include $\neg$ at its beginning), then a proof by contradiction of $P$, assumes $\neg P$ and derives absurdity.

To a classical mathematician this distinction does not exist.

✏️ Challenge

Show that we also have the converse implication that the principle of proof by contradiction entails the law of double negation. Conclude that the principle of proof by contradiction is equivalent to the law of double negation.

In Lean, the inference is named by_contradiction, and since it is a classical rule, we have to use the command open classical before it is available. Once we do so, the pattern of inference is expressed as follows:

open classical

    variable (P : Prop)

    example : P :=
    by_contradiction
      (assume h : ¬ P,
        show false, from sorry)    

One can show that the Law of Excluded Middle (LEM) implies the Law of Double Negation (DN), and therefore, it legitimizes proofs by contradiction. In fact for every proposition $P$ we show that, by the intuitionistic (aka constructive) rules of inference, from $P \lor \neg P$ we can derive $\neg \neg P \To P$. We are going to construct the proof in stages: To this end, suppose $P$ is an arbitrary proposition, and assume $P \lor \neg P$ holds. We are trying to derive the implication $\neg \neg P \To P$. Using the elimination rule for disjunction, we need to prove this implication in both cases, i.e. when $P$ holds and also separately when $\neg P$ holds. Let us show what we have achieved so far, with gaps yet to be filled shown with vertical dots, in the style of natural deduction:

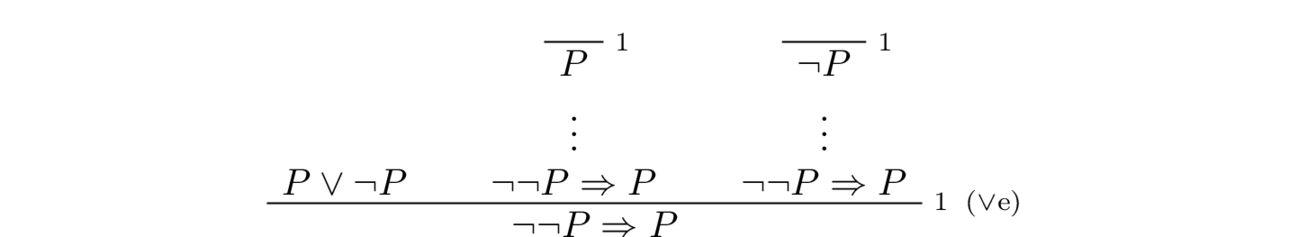
In the first case, we want to show if $P$ holds then $\neg \neg P \To P$ follows. Here we use the introduction inference rule for implication: We add the assumption $\neg \neg P$ to the context of our assumptions which now includes both $P$ and $\neg \neg P$. Of course, since $P$ holds we can trivially derive $P$ by forgetting about the second assumption. Therefore, by implication introduction, we derive $\neg \neg P \To P$. Here the hypothesis $2$ is cancelled.

Similarly, if $\neg P$ holds, and if $\neg \neg P$ holds then we derive falsity (aka contradiction) $\bot$ (how?), from which we can derive any proposition (by the principle of explosion) and in particular we can derive $P$. Again, by implication introduction, we derive $\neg \neg P \To P$. Here the hypothesis $2$ is cancelled.

Now, in both cases $P$ and $\neg P$, we have derived $\neg \neg P \To P$, and therefore, by disjunction elimination, we cancel the hypothesis $1$ and derive $\neg \neg P \To P$. ✨

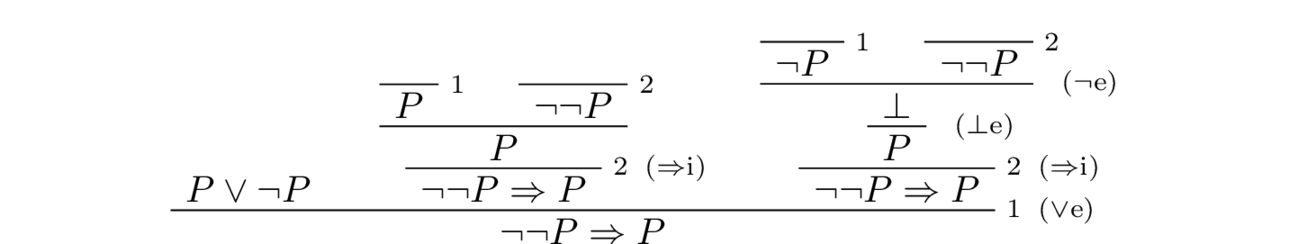
Here is Lean proof accompanying the natural deduction above:

def EM (P : Prop) : Prop := 
P ∨ ¬ P

def DN (P : Prop) : Prop :=
¬ ¬ P → P 

theorem EM_implies_DN : EM P → DN P := 
begin 
dsimp [EM, DN], 
intro emp,  
intro dnp, 
cases emp, 
{exact emp,},
{exfalso,
apply dnp,
exact emp, 
},
end  

Can you understand every step of the proof and how each step in the Lean proof correspond to an step in the natural deduction proof?

🤖 Challenge

Here is another attempt at a Lean proof of the law of Double Negation from the law of Excluded Middle, but it is not a good proof. Can you spot the flaw?

theorem another_EM_implies_DN : EM P → DN P := 
begin 
dsimp [EM, DN], 
intro emp,  
intro nnp, 
cases emp with p np, 
exact p, 
by_contradiction,
exact nnp np, 
end  

The law of Excluded Middle from the law of Double Negation

Is the converse implication

\[ (\neg \neg P \To P) \To (P \lor \neg P) \]

valid intuitionistically?

Even in constructive mathematics we can show that the negation of LEM is false.

✏️ Challenge

Show that for all propositions $P$, the proposition $\neg \neg (P \lor \neg P)$ is a tautology.

So what do constructive mathematicians believe? If we know that negation of LEM is false, surely LEM itself must be true, mustn’t it? It need not, since if the negation of a proposition, say $P$, is false, then $\neg P$ is false and therefore $\neg \neg P$ is true. But, to judge that $P$ is true from the truth of $\neg \neg P$, we need to know that the law of double negation holds for $P$ which we don’t.

Let’s highlight the observation we just made:

In constructive mathematics, if the negation of some propositions is false, it does not necessarily follow that the proposition itself is true.

So, it seems that that constructive mathematics is stranger than classical mathematics specially if we have already been used to the Law of Excluded Middle. But, are there any reasons why we should leave the comfort of our habits and give up LEM which simplifies our lives?

We shall discuss this further in class, and also in future lectures. Stay tuned! 👀