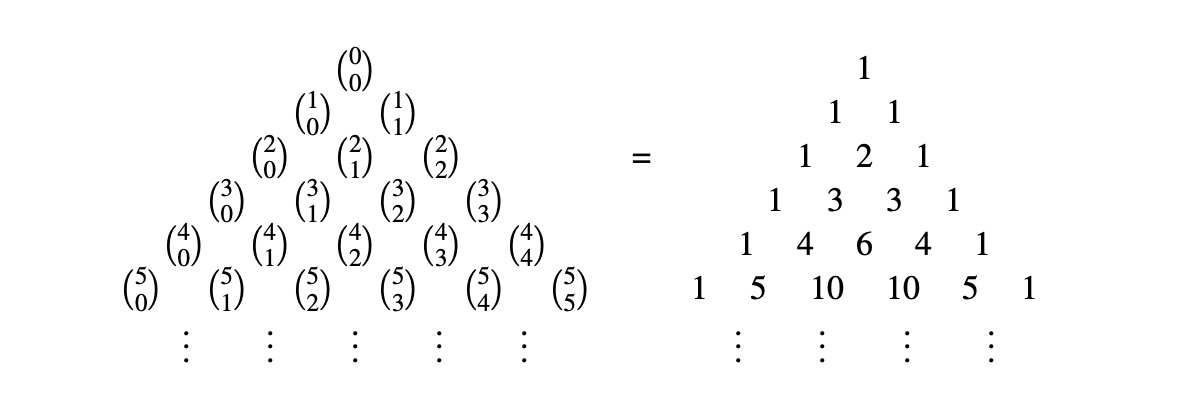Natural Numbers and The Principle of Induction

Table of contents

1. Introduction

Introduction

So far our discussion has remained constrained to logic, and we need to transition to particular mathematical objects and structures, and apply the proof strategies we have developed to our reasoning about mathematical objects. A good place to start is the natural numbers. In many foundation of mathematics, natural numbers are one of the most basic and fundamental mathematical objects and many other objects and structures of interest can be constructed from these. It is in this sense that the nineteenth century German mathematician Kronecker in a lecture proclaimed that “Natural numbers were created by God, everything else is the work of men.” ¹

Natural numbers are $0, 1, 2, 3, \ldots$ and we use the symbol $\NN$ to refer to their collection. Therefore $0$ is in $\NN$ and $1$ is in $\NN$ and so on. Here is how we define them more formally/symbolically: $\NN$ is the smallest collection that

• includes the symbol $\0$
• and if $n$ belongs to $\NN$ then the symbol $\suc(n)$ also belongs to $\NN$.

These two rules generate the following elements in $\NN$:

$\0$, $\suc(\0)$, $\suc(\suc(\0))$ and so on.

We shall use the symbols $\0$, $\1$, $\2$, $\ldots$ as shorthand for cumbersome $\suc(\0)$, $\suc(\suc(\0))$, $\ldots$. We also use $n+1$ as shorthand notation $\suc(n)$. For now these are just notation, but later, in lesson on recursion, we actually define a an operation $+$ on natural numbers and we actually prove that $n+1 = \suc(n)$.

Therefore, any element of $\NN$ is either $\0$ or some iteration of the operation $\suc$ applies to $\0$. In other words, to construct a natural number is to start with $\0$ and apply the successor operation “finitely” many times.

But it is not just enough to say that the above elements are natural numbers: We also want $\0$, $\suc(\0)$, $\suc(\suc(\0))$, $\ldots$ to be the only elements which we are going to regard as natural numbers, and nothing else. To do this end, we have to say for any property of natural numbers, it is sufficient to verify that property only on $\0$, $\suc(\0)$, $\suc(\suc(\0))$, $\ldots$.

Principle of Induction. Let $P$ be any property of natural numbers. Suppose $P$ holds of zero, and whenever $P$ holds of a natural number $n$, then it holds of its successor, $\suc(n)$. Then $P$ holds of every natural number.²

The principle of induction is expressed by the following natural deduction rule:

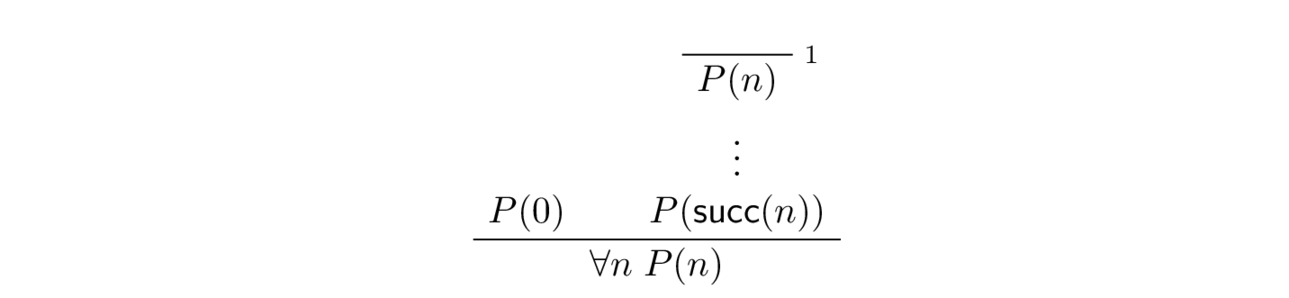
The natural deduction rule above states that in a proof by induction

• the first required task is to give a proof of $P(\0)$; this steps is called the base case,
• the second task requires temporarily fixing a natural number $n$, assuming that $P$ holds of $n$, and then showing that $P$ holds of $\suc(n)$. This task is called the induction step. In the induction step, the assumption that $P$ holds of $n$ is called the inductive hypothesis.

Then the principle of induction ensures that $P$ holds of every natural number provided that we have successfully accomplished these two task. Let us make the principle and the use of these terminologies more clear by few examples.

Theorem

For every natural number $n$, \[ 1 + 2 + \ldots + 2^n = 2^{n+1} - 1\, . \]

Proof

We prove this by induction on $n$. In the base case, when $n = 0$, we have $1 = 2^{0+1} - 1$, as required.

For the induction step, fix $n$, and assume the inductive hypothesis

\[ 1 + 2 + \ldots + 2^n = 2^{n+1} - 1\, .\]

Under this assumption, we need to prove the same equality but when $n$ replaced by $n + 1$. But this is just a calculation:

\begin{aligned} 1 + 2 + \ldots + 2^{n+1}&= (1 + 2 + \ldots + 2^n) + 2^{n+1} \\ \
\
&= 2^{n+1} - 1 + 2^{n+1} \\ \
\
&= 2 \cdot 2^{n+1} - 1 \\ \
&= 2^{n+2} - 1. \end{aligned}

The Example of Binomial Coefficient

Algebraically, the binomial coefficients are the positive integers that occur as coefficients in the expansion of the binomial power $(x + y)^n$. Commonly, a binomial coefficient is indexed by a pair $n,k$ of of integers where $n ≥ k ≥ 0$ and is written $\tbinom n k$. It is the coefficient of the $x^k y^{(n-k)}$ term in the polynomial $(x + y)^n$ and satisfies the equation \[ {\displaystyle {\binom {n}{k}}={\frac {n!}{k!(n-k)!}}.} \]

Here is a beautiful geometric illustration of the expansion of $(x+y)^k$ for $k=1,2,3$ by User:Cmglee on Wikipedia.

The binomial coefficients satisfy Pascal’s triangle identity \[ {\displaystyle {\binom {n}{k}}={\binom {n-1}{k}}+{\binom {n-1}{k-1}}.} \]

The means each entry in the triangular arrangement of the binomial coefficients in below is the sum of the two immediately above.

There is an interesting combinatorial interpretation of the binomial coefficient $\tbinom n k$: it is the same as the number of choosing $k$ objects from $n$ objects regardless of choice order. For instance to make there are $\tbinom{22}{11}$ ways to make a football team (consisting of 11 eleven players on the fields) out of 22 eligible soccer players. We defined $\binom n k$ as the coefficient of the monomial $x^k y^{(n-k)}$ term in the expansion of the polynomial $(x + y)^n$ and now we claim this is the same as number of choosing $k$ objects from $n$ objects where $k \le n$. This is because \[ (x + y)^n = (x+y) \times (x + y) \times \ldots \times (x+y) \] $n$-time, and if we use the distributivity of multiplication over addition enough times, we get terms like $x^n, x^{n-1} y,\ldots, x^k y^{(n-k)}, \ldots, y^n$ in the sum \[ x^n + x^{n-1} y + x y x^{n-2} + \ldots \] But how many times does the term $x^k y^{(n-k)}$ appear in this sum? Answer: we have to choose the term $x$ from $k$-many bracket $(x+y)$, and therefore the answer is $\binom n k$. Note that the order of this choice does not matter since by the commutativity of multiplication we have equalities such as $x y x^{n-2} = x^{n-1} y$.

We can take advantage of Pascal’s identity and define recursively

def choose : ℕ → ℕ → ℕ
| _             0 := 1
| 0       (k + 1) := 0
| (n + 1) (k + 1) := choose n k + choose n (k + 1)

#eval choose 4 0 
#eval choose 4 1 
#eval choose 4 2 
#eval choose 4 3 
#eval choose 4 4 
#eval choose 4 5 

Theorem

For every natural number $n$, \[ \displaystyle\sum_{i=1}^{n} i = \binom{n+1}{2}\]

We first prove a Lemma:

Lemma

For all natural numbers $n$ we have \[ \binom{n+1}{2} + (n+1) = \binom{n+2}{2} \, .\]

Proof of Lemma

Let $n$ be an arbitrary natural number and consider $n+2$ elements. We want to count the number of ways we can choose $2$ elements out of the total $n+2$ elements. Fix one element and call it “cookie monster”. Either cookie monster is in the selected pair or he is not. If cookie monster is selected then we only have to choose $1$ other person in $n+1$ ways since $n+1$ other people are left (excluding cookie monster). If cookie monster is not in the selected pair, then the selected pair is chosen in $\tbinom{n+1}{2}$ ways. All in all there are $\tbinom{n+1}{2} + (n+1)$ many ways to choose $2$ people out of $n+2$ people. Hence, \[ \binom{n+1}{2} + (n+1) = \binom{n+2}{2} \, . \]

Proof of Theorem

Note that the left hand side is simply the sum of the first $n$ positive natural numbers. We proceed by proof by induction with the starting point $1$. The bases case is satisfied since when $n=1$, the left hand side is $1$ and the right hand side is $\binom 2 2$ which is also $1$ (think in how many ways you can select a group of two people out of two people!). Suppose that the identity holds for a number $n$ (IH), and consider the identity for $n+1$. We want to show that
\[ \displaystyle\sum_{i=1}^{n+1} i = \binom{n+2}{2}\] By the induction hypothesis (IH), we have \[ \displaystyle\sum_{i=1}^{n} i = \binom{n+1}{2}\, .\] Now add the next term (i.e. $n+1$) to both side of this equation. Hence, \[ \displaystyle\sum_{i=1}^{n+1} i = \binom{n+1}{2} + (n+1) \, .\] Now, if we show that $\tbinom{n+1}{2} + (n+1) = \binom{n+2}{2}$ we are done by induction. But this is proved in the lemma above. $\qed$

We give another example of usefulness of the logical principle of induction, this time in proving statements about logic itself. Let’s define the width of a well-formed propositional formula to be the width of the list of the the characters that appear in it (we do not count brackets since they are only a aiding device for unique readability.) For instance, in the lesson on parsing we learned that the well-formed formula $\neg P \lor Q \To R \land S$ can be rendered as the list ["¬", "P","∨","→", "R", "∧", "S"] and after inserting the brackets it is rendered as ["(", "(", "¬", "P", ")", "∨", "Q", ")", "→", "(", "R", "∧", "S", ")"]. Therefore, the width of this list is 7. We denote the width of a formula $\varphi$ by $\mathrm{wd}(\varphi)$. In general we define the width of formulae recursively since the formulae are built from atomic propositions and connectives recursively:

1. $\wd (P) = 1$ for an atomic proposition $P$.
2. $\mathrm{wd} (\varphi \To \psi) = \mathrm{wd}(\varphi) + \mathrm{wd}(\psi) + 1$,
3. $\mathrm{wd}(\varphi \land \psi) = \mathrm{wd}(\varphi) + \mathrm{wd}(\psi) + 1 $,
4. $\mathrm{wd}(\varphi \lor \psi) = \mathrm{wd}(\varphi) + \mathrm{wd}(\psi) + 1$,
5. $\mathrm{wd}(\varphi \iff \psi) = \mathrm{wd}(\varphi) + \mathrm{wd}(\psi) + 1$,
6. $\mathrm{wd}(\neg\varphi) = \mathrm{wd}(\varphi) + 1$,

Let’s also define the height of a formula to be the height of its parsing tree. Consider for example the formula $ (P \To Q \To R) \To (P \land Q) \To R $. We observed that the parsing tree of this formula is drawn as in below:

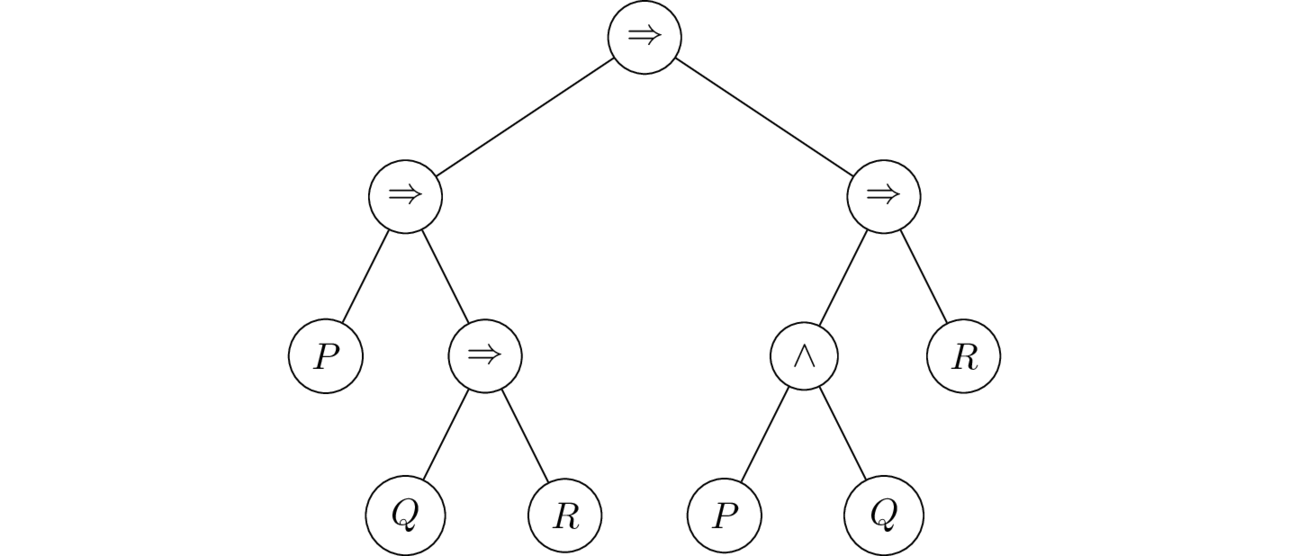
Therefore, by our definition the height of $ (P \To Q \To R) \To P \land Q \To R $ is 3.

For a formula $\varphi$ we denote its height by $\mathrm{ht}(\varphi)$. Therefore, $ \ht ( (P \To Q \To R) \To P \land Q \To R )= 3$.

To give a precise definition of $\ht$ we need to define it on formulae recursively since the formulae are built from atomic propositions and connectives recursively:

1. $\ht (P) = 0$ for an atomic proposition $P$.
2. $\ht (\varphi \To \psi) = \max(\ht(\varphi) , \ht(\psi) ) +1 $,
3. $\ht(\varphi \land \psi) = \max(\ht(\varphi) , \ht(\psi) ) +1 $,
4. $\ht(\varphi \lor \psi) = \max(\ht(\varphi) , \ht(\psi) ) +1$,
5. $\ht(\varphi \iff \psi) = \max(\ht(\varphi) , \ht(\psi) ) +1$,
6. $\ht(\neg\varphi) = \ht(\varphi) +1$.

We use the principle of induction to prove the following theorem.

Theorem (no skyscraper for propositional formulae)

For all propositional formulae $\varphi$ we have that $\ht(\varphi) < \wd(\varphi)$.

Proof

We prove this by induction on the height of formulae. If $\varphi$ has height 0 then it is an atom. Hence, $\ht(\varphi) = 0 < 1 = \wd(\varphi)$, so the base case is verified.

To prove the induction step, suppose that for all formulae $\varphi$ with $\ht(\varphi) = n$ we have $\ht(\varphi) < \wd(\varphi)$. Now, suppose $\psi$ is a formula of height $n+1$. Either

1. $\psi = \neg\varphi$ for some formula $\varphi$ with height $n$, or
2. $\psi = \varphi_1 \sqcap \varphi_2$ where $\sqcap$ is one of the connectives $\To, \lor, \land$.

In the first case, we have \[ \ht(\psi) = \ht(\varphi) + 1 < \wd(\varphi) + 1 = \wd(\psi) \] In the second case, we also infer $\ht(\psi) < \wd(\psi)$ since $\ht(\psi) = \ht(\varphi_1 \sqcap \varphi_2)$ and $ \wd(\psi) = \wd(\varphi_1 \sqcap \varphi_2)$, by rewriting $\psi$ as $\varphi_1 \sqcap \varphi_2$, and since \[ \ht(\varphi_1 \sqcap \varphi_2) = \max(\ht(\varphi_1) , \ht(\varphi_2) ) +1 < \max(\wd(\varphi_1), \wd(\varphi_2)) + 1 < \wd(\varphi_1)+ \wd(\varphi_2) + 1 < \wd(\varphi_1 \sqcap \varphi_2) \] Because both $\varphi_1$ and $\varphi_2$ have height $n$ or smaller, by the induction hypothesis $\ht(\varphi_1) < \wd(\varphi_1)$ and $\ht(\varphi_2) < \wd(\varphi_2)$.

That is why parsing trees are more like pyramids than skyscrapers.

Footnotes